Fundamentals

4.1. Fundamentals#

Thermodynamics is the branch of physics that focuses on describing the macroscopic changes in energy and work of a system. In classical thermodynamics, the behaviour of macroscopic systems is governed by a set of laws, which were derived from empirical observations. At first, the laws of thermodynamics were built on the basis of properties of the system that could be measured (e.g. temperature, volume, pressure), and no connection with theories concerning the molecular nature of the matter existed.

Later, however, the approach based on statistical mechanics provided linkages between molecular interactions and their manifestations in the macroscopic observable properties of a system. This lead to what is referred to as statistical thermodynamics. By means of the statistical approach, it is possible to derive all the laws of thermodynamics, as well as all the thermodynamic properties, based on the description of the microscopic states of a system.

Systems#

In a thermodynamic analysis it is essential to define the investigated system and its interactions with the surroundings. A system can be any region that is clearly defined in terms of spatial coordinates, which can be fixed or moving. The boundary is the surface delimiting this region, and it can be an actual wall or an imaginary surface. The external region to the system boundary is called the environment or surroundings.

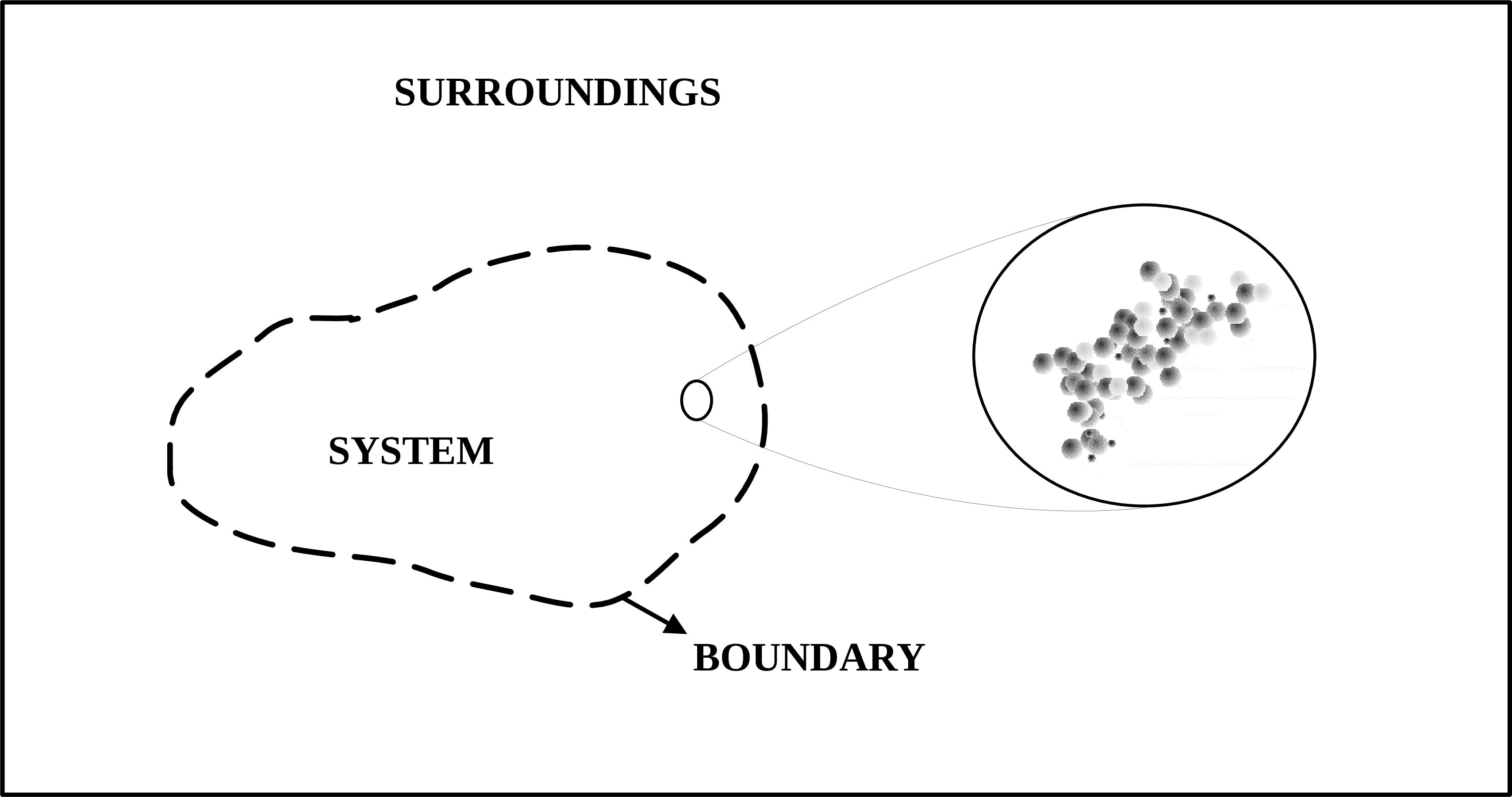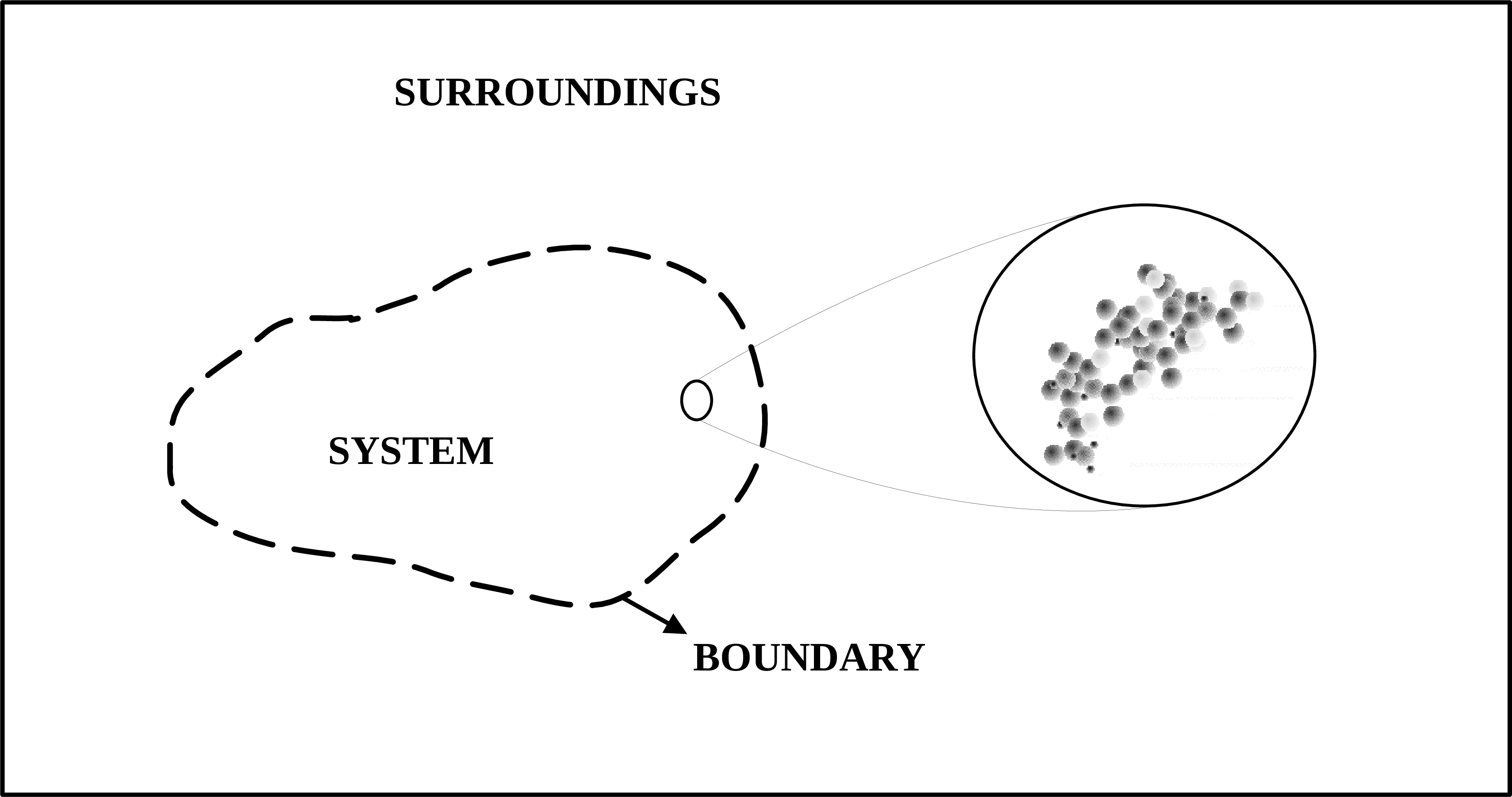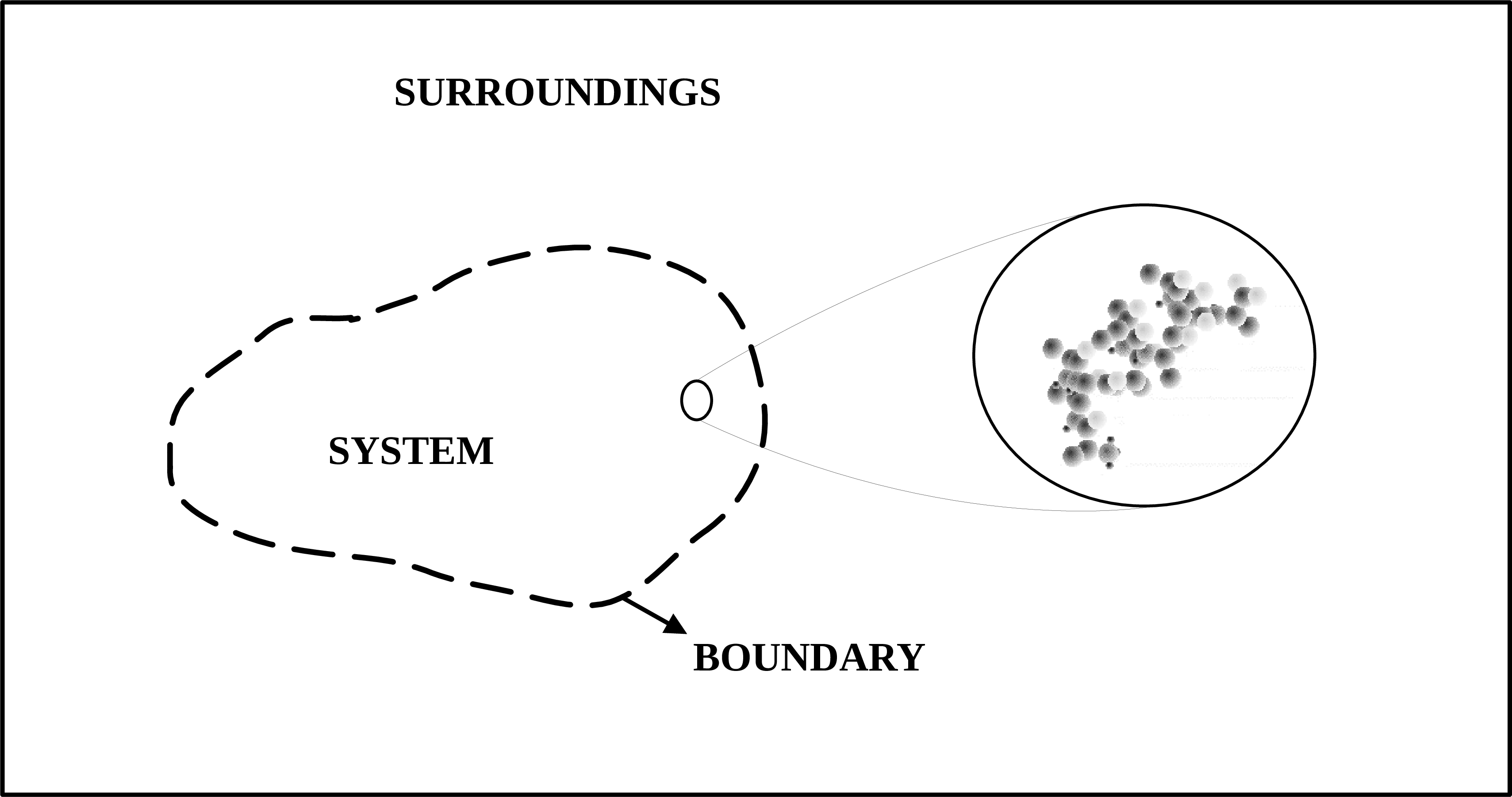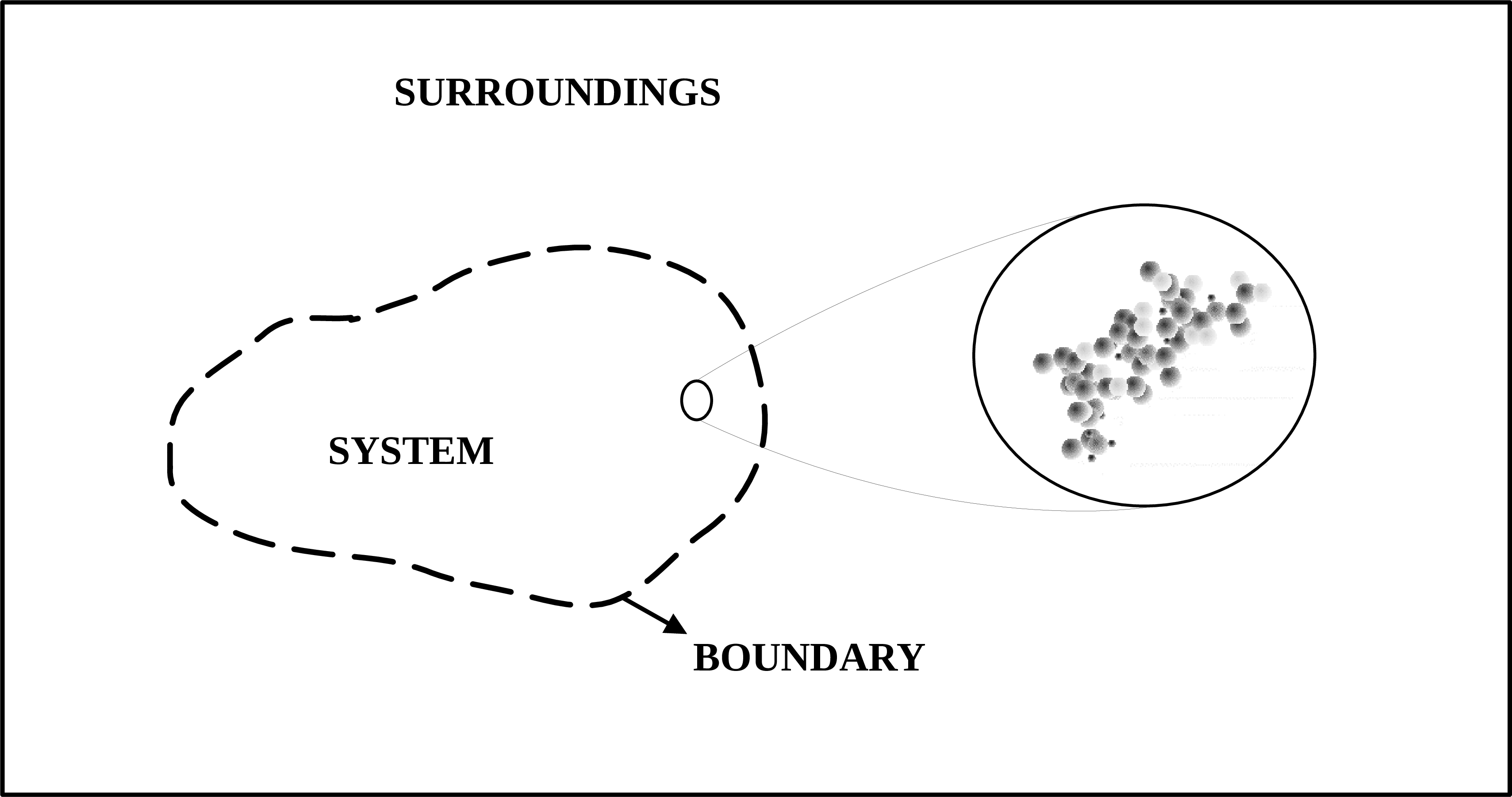
../../../_images/system.gif — Fig. 4.1 Thermodynamic system. Source: Adapted from Wikkimedia Commons.#

The state of a thermodynamic system is typically expressed by means of its primitive properties, which refer to the characteristics of the system that can be experimentally measured. For example:

pressure, \(\mf p\),
volume, \(\mf V\), and
temperature, \(\mf T\).

If a system that is initially at a stable equilibrium state interacts with the surroundings, it can undergo a change of state. This is usually characterised by a change in at least one primitive property of the system.

State functions#

In order to describe the change of state of a system, derived properties are used. They are also functions of state, or simply state functions, and therefore they depend only on the specified state of the system, regardless of the path taken to get to this state.

Some examples of function of states are:

internal energy, \(\mf U\): the sum of kinetic and potential energy of all microscopic particles composing the system;
enthalpy, \(\mf H\): the sum of internal energy of the system and the product of its pressure and volume; and
entropy, \(\mf S\): degree of disorder or uncertainty of a system.

Process functions#

As opposed to functions of state, process functions describe the path or the process involved in a change of state of the system. A system can interact with the surroundings to change its state through the following process functions:

work, \(\mf W\), e.g. mechanical or electrical work, like the compression or expansion of a volume due to a moving piston,
heat, \(\mf Q\), e.g. energy transfer due to a temperature difference.

Intensive vs extensive properties#

Properties of a system can be further classified as intensive or extensive. By convention, extensive properties are those depending on the size (extension) of the system, whereas intensive properties do not depend on the system’s extension. Some examples of extensive properties are volume and enthalpy. Temperature and pressure are on the other hand are intensive, because they are independent of the system’s size.

Extensive properties can be converted into intensive properties by dividing their value by the system’s mass or number of moles. For example, it is common that enthalpy is given as specific enthalpy, that is, in units of energy per units of mass (\(J/kg\) in SI units). Alternatively, if a property such as enthalpy is given in units of energy per moles (\(J/mol\) in SI units), it is called molar enthalpy.

Classification of boundaries#

The interactions between a system and the surroundings are determined by the nature of the system boundary. There are four definitions of boundaries, which are linked to different types of interactions between the system and the surroundings:

closed: no mass flow, possibility for heat flow (\(\mf \Delta Q\neq 0\)) and / or work to be done (\(\mf \Delta W\neq 0\));
open: possibility for mass and heat flow, as well as for work to be done;
adiabatic: no heat or mass flow (\(\mf \Delta Q=0\)), yet work can to be done (\(\mf \Delta W\neq 0\)); and
isolated: no mass flow, no heat flow (\(\mf \Delta Q=0\)) and no work done (\(\mf \Delta W=0\)).

Temperature#

Thermodynamic temperature is an expression to characterise the random (thermal) motion of the particles. In general all interacting thermodynamic systems try to equal their temperatures by an energy flow, i.e. heat. This means, that if two systems with different temperatures are brought togehter, the induced heat flow will reduce the temperature of the warmer system and increase the temperature of the colder system. The heat flux is always from the higher to the lower temperature.

In a thermodynamic equilibrium, there are no heat or mass flows between interacting systems, i.e. the state quatities do not change in time. This implies a thermal equilibrium, the state at which the systems have the same temperature. A single system is in thermal equilibrium if the temperature is homogenous and does not change with time.

The SI-unit of temperature is Kelvin, where \(\mf 0~K\) is the absolute lowest temperature and \(\mf 0~^\circ C\) corresponds to \(\mf 273.15~K\). Temperature differences have the same values in Kelvin as in Celsius.

At finite temperature, the particles in a system do not have the same velocity, but a distributed over a broad range. This is an important aspect, as many chemical reactions require the involved particles to overcome the activation energy. Thus, there is always a probability that a particle has the needed kinetic energy. This velocitiy distribution, the Maxwell-Boltzmann distribution, depends only on the temperature and the gas properties:

\[ \mf f(v) = 4\pi v^2 \left(\frac{m_M}{2\pi k_B T}\right)^{\frac{3}{2}} \cdot e^{\left(-\frac{m_M v^2}{2 k_B T}\right)}\quad , \]

with \(\mf m_M\) the mass of a single particle and the Boltzmann constant \(\mf k_B \approx 1.38\cdot 10^{-23}~ J/K\).

The most probable velocity \(\mf v_p\) is given by

\[ \mf v_p = \sqrt{\frac{2k_B T}{m_m}}, \]

the mean velocity \(\mf \bar{v}\) is

\[ \mf \bar{v} = \sqrt{\frac{8k_B T}{\pi m_m}}, \]

and the velocity with the median kinetic energy \(\mf v_m\) can be computed as

\[ \mf v_m = \sqrt{\frac{3k_B T}{m_m}}\quad . \]

The integration of the velocity distribution leads to the probability for a particle to have a velocity in the integration range. The distribution function at two temperatures is shown in Fig. 4.2.

../../../_images/maxwell.svg — Fig. 4.2 Maxwell’s velocity probability density function.#

Ideal Gases#

Ideal gases represent the assumption that the particles have a very small volume, i.e. can be treated as point particles, and the gas volume contains a large number of same particles. Additionally, there are no forces interacting between the particles – but the idealised (elastic, instant) collisions with each other and the system boudaries.

Equations of state relate various state quantities, as they are in general not independent. In the case of an ideal gas, the following equation of state – called (classical) ideal gas law – can be used:

\[ \mf pV = n R T \]

where \(\mf n\) respresents the number of moles in the system and \(\mf R \approx 8.314~J/(mol~K)\) is the universal gas constant. A mole is defined by the Avogadro constant, as \(\sf N_A \approx 6.02\cdot 10^{23}~1/mol\) being the number of particles in a mole.

Heat Capacity#

To (infinitesimally) increase the temperature of a system by \(\mf dT\), the following amount of heat \(\mf \Delta Q\) is needed

\[ \mf \Delta Q = C\cdot dT \]

where \(\mf C\) is the heat capacity. The correspondig (mass) specific quantity is \(\mf c\). In general this material dependent quantity is temperature-dependent, \(\mf C=C(T)\), thus the heat needed to change a system’s from temperature \(\mf T_1\) to \(\mf T_2\) is

\[ \mf Q_{12} = \int_{T_1}^{T_2} C(T)\ dT \]

The specific values depend on the process itself, thus the two following specification need to be considerd:

isochoric, i.e. the volume stays constant during the process \(\mf \Delta V=0\), \(\mf c_V\), the heat flux does change only the internal energy, and
isobaric, i.e. the pressure stays constant \(\mf \Delta p=0\), \(\mf c_p\), where the heat flux can change the internal energy and can do work.

Both values are related:

\[ \mf c_p - c_v = \frac{R}{M} \]

where \(\mf M\) is the molar mass and

\[ \mf \frac{c_p}{c_v} = \gamma \]

where \(\mf \gamma\) is called the heat capacity ratio.

For isobaric processes, the change of enthalpy for a given heat amount is given by

\[ \mf dH = \Delta Q \big|_{\text{at}\ dp=0} = m c_p dT\quad . \]