FDS Overview

FDS describes itself as:

The software described in this document, Fire Dynamics Simulator (FDS), is a computational fluid dynamics (CFD) model of fire-driven fluid flow. FDS solves numerically a form of the Navier-Stokes equations appropriate for low-speed (Ma < 0.3), thermally-driven flow with an emphasis on smoke and heat transport from fires.
– FDS User’s Guide

It is a widely used CFD software in fire safety science.

• freely available and open source

• runs on Linux / Windows / OSX

• very well documented with accompanying verification and validation guides

Note

The lecture notes use FDS in version 6.7.5, so that specific information may not be valid for other version of FDS.

Please refer always to the documentation provided for your version of FDS. All documents can be found here: NIST/fds-smv.

Included models in FDS

Fluid dynamics

• adopted form of Navier-Stokes for low speed and thermally driven flows

• emphasis on smoke and heat transport from fires

• LES model, DNS possible

• explicit predictor-corrector scheme, second order in time and space

Combustion

• single step, mixing controlled chemical reaction

• lumped species (air, fuel and products)

• options for more complex reactions

Radiation transport

• gray gas assumption, or wide band model possible

• finite volume method with discrete angles (default 100)

• absorption coefficients are based on a narrow band model (RadCal)

Geometry

• rectilinear meshes, rectangular obstructions

• complex geometries

Parallel Execution

• multiple messes possible and needed for distributed computing

• MPI and OpenMP parallel

Boundaries

• thermal boundary conditions

• burning behavior (pyrolysis)

• heat conduction in obstructions

Governing equations

\[ \mf \frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \textbf{u}) =0 \]

\[ \mf \frac{\partial \rho Y_{\alpha}}{\partial t} + \nabla \cdot (\rho Y_{\alpha}\textbf{u}) = - \nabla \cdot \textbf{J}_{\alpha} + \dot{m_{\alpha}'''} \]

\[ \mf \frac{\partial \rho \textbf{u}}{\partial t} + \nabla \cdot (\rho \textbf{uu}) = -\nabla p + \nabla \cdot \textbf{T} + (\rho - \rho_0)\textbf{g} \]

\[ \mf \frac{\partial \rho h_s}{\partial t} + \nabla \cdot (\rho h_s \textbf{u}) = \frac{D\bar{p}}{Dt} + \dot{q}''' - \nabla \cdot \dot{\textbf{q}}'' \]

\[ \mf \rho = \frac{\bar{p}\overline{W}}{RT} \]

Variable	Quantity
\(\mf \rho\)	mass density
\(\mf \textbf{u}\)	velocity
\(\mf Y_{\alpha}\)	mass fraction of species \(\mf \alpha\)
\(\mf \textbf{J}_{\alpha}\)	diffusive mass flux of \(\mf \alpha\)
\(\mf \dot{m}_{\alpha}'''\)	reaction source term
\(\mf T\)	deviatoric stress tensor
\(\mf g\)	gravitational acceleration
\(\mf h_s\)	sensible enthalpy per unit mass
\(\mf \dot{q}'''\)	heat release per unit volume due to reaction
\(\mf \dot{q}''\)	heat flux (diffusion, conduction and radiation)
\(\mf \bar{p}\)	thermodynamic pressure
\(\mf \overline{W}\)	mixture molecular weight
\(\mf T\)	temperature
\(\mf R\)	ideal gas constant

The momentum equation may be rewritten as

\[ \mf \frac{\partial \textbf{u}}{\partial t} = -(\textbf{F}+\nabla H), \]

\[ \mf \textbf{F} = \underbrace{\textbf{u} \cdot \textbf{u} - \nabla K}_{-\textbf{u}x(\nabla x \textbf{u})} - \bar{p}\nabla(1/\rho)-\frac{1}{\rho}[\nabla \cdot \textbf{T}+(\rho - \rho_0)\textbf{g}], \]

\[ \mf H \equiv \bar{p}/\rho + K, \]

with the resolved kinetic energy per unit mass \(\mf K \equiv \frac{1}{2}\left|\textbf{u}\right|^2\). the Bernoulli intefral \(H\) obeys the following Poisson equation

\[ \mf \nabla^2H = - \left[ \nabla \cdot \textbf{F} + \frac{\partial}{\partial t}(\nabla \cdot \textbf{u}) \right]\quad . \]

One way to compute the divergence is given by differentiating the equation of state, which leads to

\[\begin{split} \mf \begin{align} \nabla \cdot \textbf{u} &\mf = \left(\frac{1}{\rho c_pT}-\frac{1}{\bar{p}}\right) \frac{D \bar{p}}{Dt}\\ &\mf + \frac{1}{\rho c_pT}[\dot{q}'''-\nabla \cdot \dot{\textbf{q}}'']\\ &\mf + \frac{1}{\rho}\sum_{\alpha}\left(\frac{\overline{W}}{W_{\alpha}} - \frac{h_{s,\alpha}}{c_pT}\right)[\dot{m}_{\alpha}'''-\nabla \cdot \textbf{J}_{\alpha}]\end{align} \end{split}\]

Numerical scheme

1. update the density equation to obtain \(\rho^{n+1}\)

2. update the \(n_s - 1\) species equations to get \(Y^{n+1}_{\alpha}\)

3. Update the temperature from equation of state to obtain \(T^{n+1}\)

4. Compute \((\nabla \cdot \textbf{u})^{n+1}\)

5. Solve the Poisson equation for \(H^n\)

6. Use above pressure solution to update the velocity \(\textbf{u}^{n+1}\)

Combustion models

• single-step, mixing-controlled combustion, simple chemistry model,reaction is assumed to be of following form

  \[ C_xH_yO_zN_v + \nu_{O_2} O_2 \rightarrow \nu_{H_2O} H_2O + \nu_{CO} CO + \nu_{s} soot + \nu_{N_2} N_2 \]

• comple stoichiometry

• finite rate combustion

Ventilation

• supply and exhaust vents

• heaters

• HVAC systems

• Fires and flows in the outdoors

FDS Guides

The FDS guides and documentation for version 6.7.5 can be found in this release.

User’s Guide

An about 400 pages thick manual to introduce users to FDS [MHF+20d]. It covers the user aspects of

• basics of FDS, getting started

• structure of FDS input files

• building geometric models

• fire and thermal boundary conditions

• ventilation

• combustion and radiation

• particles and droplets

• deices and control logic

• output

Technical guide

This document (about 175 pages) covers the technical / mathematical / scientific description of the FDS model [MHF+20a]. It includes a detailed description (or references) of the following aspects:

• general overview of the FDS model

• mass, species and enthalpy transport

• momentum transport and pressure

• combustion

• thermal radiation

• solid phase

• Lagrangian particles

• fire detection devices and HVAC

Verification and validation

To demonstrate the applicability of the FDS model, there exist two documents (in total over 1000 pages) about model verification [MHF+20b] and validation [MHF+20c]. All test are run every night to check the impact of source code changes.

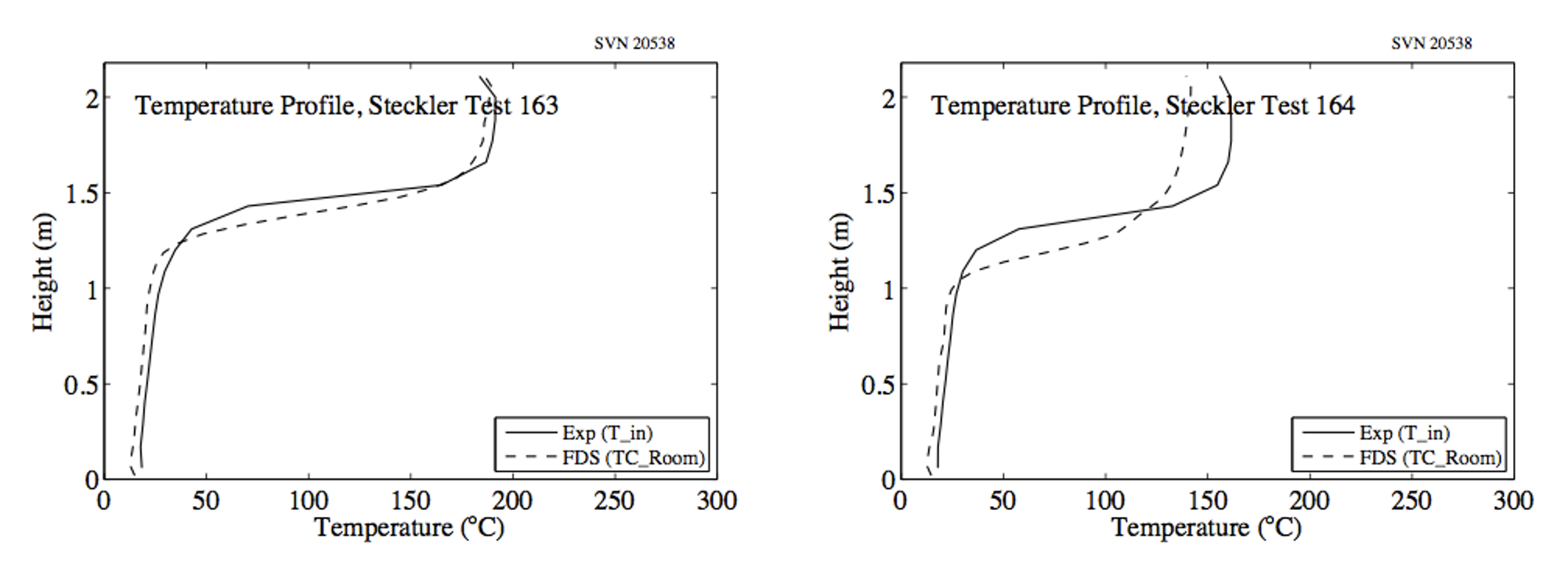
Fig. 11 Geometry and dimensions of the room.

Smokeview - Visiualisation

Smokeview (SMV) describes itsef as:

Smokeview is a scientific software tool designed for visualizing numerical predictions generated by fire models such as the Fire Dynamics Simulator (FDS).
– Smokeview User’s Guide

The manuals for Smokeview are located at the same page as the FDS documentation: NIST/fds-smv.

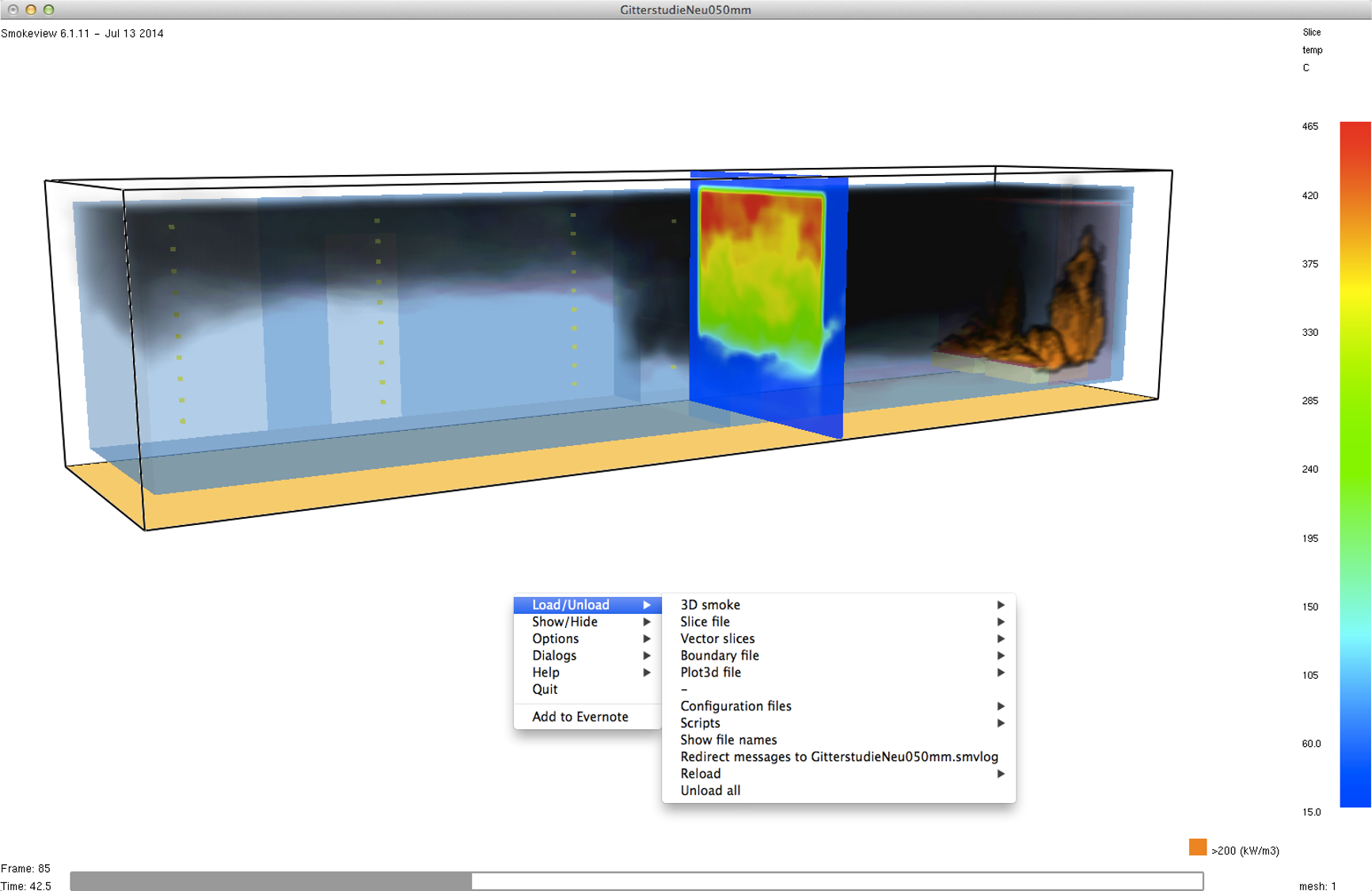
Fig. 12 Smokeview demo.

Installation

Source Code and Binary Download

The full source code (both FDS and Smokeview) is available at GitHub. This page also includes references to:

• binaries for Linux / Windows / OSX

• all manuals

• mailing lists

• verification and validation data

The software can also be found here and be downloaded for installation: NIST/fds-smv.

Installation

Please see chapter 2 (Getting Started) of [MHF+20d].

Execution

Please see chapter 3 (Running FDS) of [MHF+20d] for details how to run FDS on varioius operating systems.

Options for Graphical User Interfaces

Here two options for graphical interfaces to build FDS input files are mentioned.

A free and open source option is developed by Emanuele Gissi. It is called BlenderFDS and built as an addon to the free and open source 3D content creation suite Blender. Blender is a very powerful tool, aimed at 3d artists and different from CAD tools used in engineering disciplines. This can lead to a relatively steap learning curve.

A proprietary software, commonly used in the fire safety engineering industry, is PyroSim by Thunderhead Engineering.