5.1. Fundamentals

Burning Candle

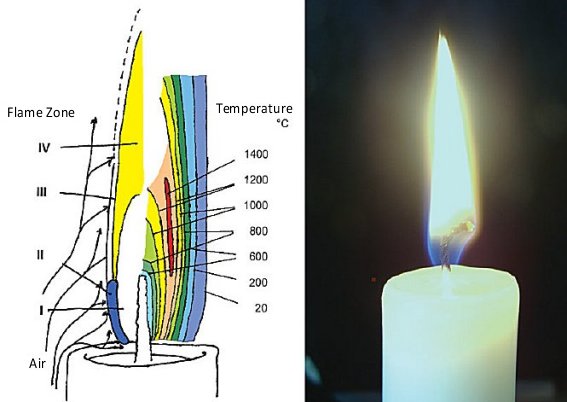
A buring candle is a good fire example. Here, once ignited, the flame emits heat radiation which is absorbed by the candle body. The solid melts and the fluid wax is transported through the wick and evaporates in a endotermic reaction. Through diffusion, the vaporised wax mixes with air and conducts an exothermic reaction, the combustion. The hot combustion products rise and eventually lead to further reactions.

The main zones of this process and the characteristic temperatures are shown in Fig. 5.1, with:

• Zone I: Endotermic vaporisation of the wax,

• Zone II + III: Decomposition of the wax molecules, diffusive mixing with the ambient air and combustion, and

• Zone IV: Hot (large) soot particles emit thermal radiation.

Fig. 5.1 Schematics of a burning candle. Source: [Rot11].

Requirements

Combustion is a chemical reaction which basically involves three substances: fuel, oxygen and combustion products. It is

• a fast oxidation process,

• the creation of combustion products out of oxygen and fuel,

• typically based on exothermic processes, but not exclusively, and

• in total exotherm for natural fires.

In order to have a sustained fire, multiple criteria must be satisfied. They are illustrated by the fire tetrahedron, see Fig. 5.2. Thus a fire needs,

• the fuel,

• an oxydant, here oxygen, which reacts with the fuel and converts chemical bound energy into heat,

• a supply of heat, which is needed to overcome the activation energy of the chemical reaction, and

• sufficiently high reaction rates to keep up a chain reaction.

Fig. 5.2 The fire tetrahedron. Source: Wikimedia Commons.

Stoichiometry

A stoichiometric amount or stoichiometric ratio of a reagent is the optimum amount or ratio where, assuming that the reaction proceeds to completion:

1. All of the reagent is consumed

2. There is no deficiency of the reagent

3. There is no excess of the reagent

The general stoichiometric reaction for a fire is:

\[ \mf fuel + oxidant \rightarrow products \quad . \]

Stoichiometric Reaction for Methane

In many of the examples used in this lecture, methane is used as fuel. Methane is commonly used in everyday life. It is used for heating, cooking and propulsion. Liquified natural gas (LNG) is predominantly methane.

A methane molecule (\(\mf CH_4\)) consists out of four hydrogen atoms (\(\mf H\)) and a single carbon atom (\(\mf C\)), see Fig. 5.3. Methane is rarely found in Earth’s atmosphere (\(\mf 1.75~ppm\)).

Fig. 5.3 A methane molecule. Source: Wikimedia Commons.

The stoichiometric one step reaction of methane (\(\mf CH_4\)) and oxygen (\(\mf O_2\)) into carbon dioxide (\(\mf CO_2\)) and water (\(\mf H_2O\)) is given by

\[ \mf CH_4 + 2O_2 \rightarrow CO_2 + 2H_2O \quad . \]

The reaction equations relate the involved relative number of particles, i.e. in the above equation one (mole) of methane would react with two (moles) of oxygen molecules, as illustrated in Fig. 5.4.

Fig. 5.4 The combustion of methane. Source: Wikimedia Commons.

This reaction represents the ideal case (stoichiometric) where all gases are in exactly equivalent proportions. The same equation in (synthetic) air, with 21% oxygen and 79% nitrogen (\(\mf N_2\)), transforms into

(5.1)\[ \mf CH_4 +2O_2 +2 \frac{79}{21} N_2 \rightarrow CO_2 +2H_2O+2 \frac{79}{21} N_2 \quad . \]

Task

Show that the combustion of \(\mf 1~g\) methane requires about \(\mf 17~g\) of air. Check the molar masses of the involved molecules in reaction (5.1).

Heat of Combustion

During combustion, not only chemical bounds are rearagend, but in general also heat is released. This is quantified as heat of combustion \(\mf \Delta H_c\). The experimental setup used to determine the heat of combustion is the bomb calorimeter, like schematicly outlined in Fig. 5.5. Here, the heat released by the reaction increases the temperature of the system. The measurement is based on the following assumptions:

• constant volume,

• pure oxygen combustion,

• adiabatic system, and

• measure all heat transferred into the system.

Fig. 5.5 A schematic representation of a bomb calorimeter. Source: Wikimedia Commons.

Besides the explicit measurement of the heat of combustion, its value can be computed using the concept of the heat of formation \(\mf \Delta H_f\). The heat or enthalpy of formation describes the change of enthalpy required to create a mole of a molecule out of its composing atoms. The difference in the formation enthalpies of the reactants and the producs is the enthalpy released in the reaction.

The following table provides some selected value examples for the heat of combustion and heat of formation at standard conditions \(\mf \Delta H_f^0\), i.e. \(\mf 25~^\circ C\) and \(\mf 100~kPa\).

Table 5.1 Molar masses (\(\mf m_M\)), enthalpies of combustion \(\mf \Delta H_c\) and formation \(\mf \Delta H_f^0\) (approximated values)

Molecule	\(\mf m_M~/~g/mol\)	\(\mf -\Delta H_c~/~MJ/kg\)	\(\mf -\Delta H_f~/~kJ/mol\)
hydrogen, \(\mf H_2\)	2	120	0
methane, \(\mf CH_4\)	16	50	75
oxygen, \(\mf O_2\)	32	–	0
oxygen, monoatomic, \(\mf O\)	16	–	-249
nitrogen, \(\mf N_2\)	28	–	0
water, gas, \(\mf H_2O\)	18	–	242
carbon dioxide, \(\mf CO_2\)	44	–	393

A more comprehensive list is provided at Wikipedia/Standard enthalpy of formation.

Reaction Rates

A chemical process is the collision and interaction of molecules of the involved species. Therefore the rate at which the reaction takes place is proportional to the collision frequency \(\mf R\):

\[ \mf R = k C_{f}C_{o}\quad , \]

where \(\mf k\) is the specific reaction rate constant and \(\mf C_f\) and \(\mf C_o\) are the fuel and oxygen concentrations.

The reaction rate does not depend on the concentrations, but only on the temperature and may be expressed in terms of the Boltzmann factor.

\[ \mf k = A_0 \cdot \underbrace{exp\left(-\frac{E_a}{k_B T}\right)}_{Boltzmann factor}\quad , \]

with an activation energy \(\mf E_a\).

Commonly the collision frequency is taken as a power law:

\[ \mf A_0 = AT^n \]

Therefore the reaction rate is determined by the Arrhenius equation:

(5.2)\[ \mf k = AT^n exp\left(-\frac{E_a}{k_B T}\right) \]

given the pre-exponential factor \(\mf A\), the power \(\mf n\) and the activation energy \(\mf E_a\). The parameters \(A\), \(n\) and \(E_a\) for a few reactions are given in the following table.

Table 5.2 Parameters for some selected reactions (approximated values)

Reaction	\(\mf A\)	\(\mf n\)	\(\mf E_a\)
\(\mf H + O_2 \rightarrow OH + O\)	\(\mf 2.00e14\)	\(\mf 0.0\)	\(\mf 7.03e4\)
\(\mf CH_4 + O \rightarrow CH_3 + OH\)	\(\mf 6.92e08\)	\(\mf 1.56\)	\(\mf 3.55e04\)
\(\mf CH_3 + O \rightarrow CH_2O + H\)	\(\mf 8.43e13\)	\(\mf0.0\)	\(\mf0.0\)
\(\mf CH_2O + OH \rightarrow CHO + H_2O\)	\(\mf 3.43e09\)	\(\mf 1.18\)	\(\mf 1.87e03\)
\(\mf CHO + O \rightarrow CO + OH\)	\(\mf 3.00e13\)	\(\mf 0.0\)	\(\mf 0.0\)
\(\mf CO + OH \rightarrow CO_2 + H\)	\(\mf 4.40e06\)	\(\mf 1.5\)	\(\mf 3.08e03\)

The above equation (5.2) is the (modified) Arrhenius equation and it allows to predict non ideal and intermediate reactions. The stated reaction equation for methane

\[ \mf CH_4+2O_2 \rightarrow CO_2 + 2H_2O \]

is only an effective resulting representation. The actual process involves 19 reactions, each with different reaction rates.

\[\begin{split} \begin{align} \mf CH_4+ M* &\rightarrow\mf CH_3 + H + M \\ \mf CH_4 + O_2 &\rightarrow\mf CH_3 + HO_2 \\ \mf CH_4 + HO_2 &\rightarrow\mf CH_3 + 2 OH \\ \mf CH_4 + OH &\rightarrow\mf CH_3 + H_2O \\ \mf O_2 + H &\rightarrow\mf O + OH \\ \mf CH_4 + O &\rightarrow\mf CH_3 + OH \\ \mf CH_3 + O_2 &\rightarrow\mf CH_2O + OH \\ \mf CH_2O + O &\rightarrow\mf CHO + OH \\ \mf CH_2O + OH &\rightarrow\mf CHO + H_2O \\ \mf CH_2O + H &\rightarrow\mf CHO + H_2 \\ \mf CHO + O &\rightarrow\mf CO + OH \\ \mf CHO + OH &\rightarrow\mf CO + H_2O \\ \mf CHO + H &\rightarrow\mf CO + H_2 \\ \mf H_2 + O &\rightarrow\mf H + OH \\ \mf H_2 + OH &\rightarrow\mf H + H_2O \\ \mf CO + OH &\rightarrow\mf CO_2 + H \\ \mf H + OH + M &\rightarrow\mf H_2O + M* \\ \mf H + H + M &\rightarrow\mf H_2 + M* \\ \mf H + O_2 + M &\rightarrow\mf HO_2 + M* \end{align} \end{split}\]

Flammability

Not all mixtures of fuel and oxygen / air are flammable. In general there exists a lower (LFL) and an upper flammability limit (UFL), which relate the volume fraction of the fuel to air. Additionally the gas temperature may have a lower limit and there exist an autoignition temperature. A pilot ignition is needed below the autoignition temperature (AIT). The schematics in Fig. 5.6 outline the relevant regions of fuel mixture and gas temperature.

Fig. 5.6 Flammability regions.

TODO: Add link to video of autoignition of candle wax vapour

The following table outlines some flammability limits.

Table 5.3 Flammability quantities (approximated values)

Fuel	LFL	UFL	AIT / \(\mf ^\circ C\)
methane	0.05	0.15	580
propane	0.02	0.10	480
hydrogen	0.04	0.75	500

During the combustion process air’s oxygen is consumed and therefore the situation of an under-ventilated fire (not enough oxygen) is possible. Here the combustion will be reduced, however the fuel is still in the air and may burn at an other place or when oxygen is advected.

The equivalence ratio \(\mf \Phi\) relates the real ratio of the mass fractions of fuel \(\mf Y_f\) and air \(\mf Y_a\) to their stoichiometric ratio.

\[ \mf \Phi = \frac{Y_f / Y_a}{\left(Y_f / Y_a\right)_{stoichiometric}} \]

The value of \(\mf \Phi\) allows to formulate the following distinctions:

• \(\mf \Phi = 1\): ideal, stoichiometric

• \(\mf \Phi > 1\): fuel rich

• \(\mf \Phi < 1\): fuel lean

In fuel rich fires, the chances that intermediate combustion products are not involved in further reactions are high. These are mostly situations when e.g. \(\mf CO\) and soot are produced.

Flames

A flame is the region where the combustion process occures. In general, two types of combustion are considered:

• premixed: the fuel and oxygen are mixed in a combustable ratio; the chemical reaction can occur everywhere, depending on the required temperature

• non-premixed: fuel and oxygen are separated, only at the contact surface a combustable mixture may form

Natural fires are of the non-premixed type.

In premixed combustion, a localised ignition will trigger a spreading flame. The localised flame region propagates across the volume with the burning velocity \(\mf S_u\). In addition, this movement can be overlapped by advection with velocity \(\mf v_0\). The following quasi-onedimensional setup in Fig. 5.7 illustrates this setup.

Fig. 5.7 Advection opposed to burning velocity.

If the combustible gas is injected, e.g. out of a burner, with velocity \(\mf v_0\), then the following situations can occur:

• \(\mf S_u = v_0\) : a stable flame forms,

• \(\mf S_u < v_0\) : the flame is blown off,

• \(\mf S_u > v_0\) : the flame flashes back to the burner.

This phenomena can be also observed for a just extinguished candle, see following videos.

TODO: Add link to video of a candle blown off

TODO: Add link to video of a candle flash back

The following figures illustrate a setup with a pipe, which is closed at one side and filled with a combustible mixture. The velocity at which the flame effectivle moves depends on the ignition location.

Fig. 5.8 Ignition at the open end.

Fig. 5.9 Ignition at the closed end.

TODO: Add link to video of the above experiment

The combustion process is divided into two stages:

• preheat region: heat transfer from the flame heats up the unburned gas to its autoignition temperature, and

• reaction / flame region: the chemical reaction which released heat needed for the preheat region.

The qualitative form of the temperature and gas concentrations in the vicinity of a flame is shown in Fig. 5.10.

Fig. 5.10 The temperature profile, with the ambient \(\mf T_0\), the autoignition \(\mf T_i\) and the final \(\mf T_b\) temperature values, and concentration profiles. Source: [Dry11].

The chemical components as well as the reaction rates are visualised in the following figures. Here, a propane-oxygen-argon flame is shown, with

• \(\mf 1.38\%\) propane (\(\mf C_3H_8\)),

• \(\mf O_2 / Ar = 15.85\)

• empty circle: \(\mf 4 \times CO_2\)

• half circle: \(10 \times CO\)

• full circle: \(10 \times C_3 H_8\)

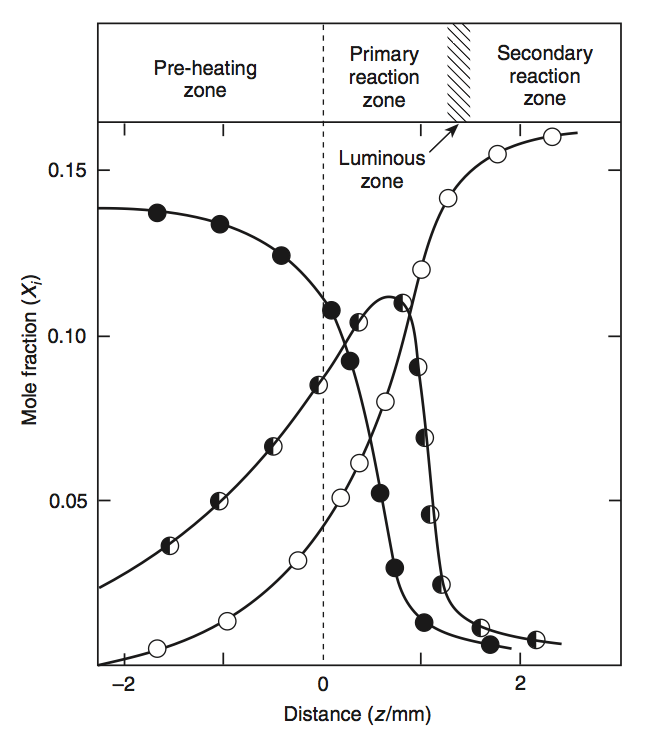
Fig. 5.11 Concentration in a propane-oxygen-argon flame. Source: SFPE Handbook.

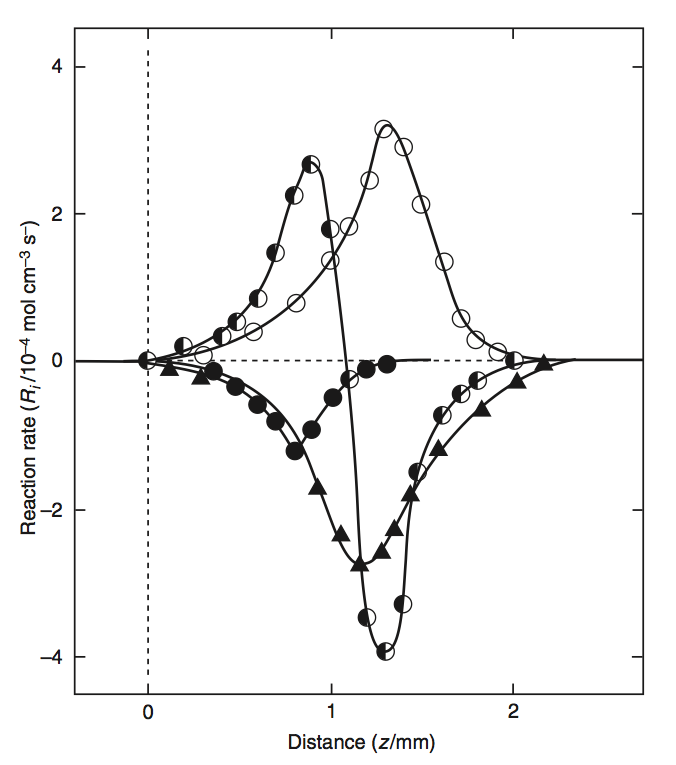
Fig. 5.12 Reaction rates in a propane-oxygen-argon flame. Source: SFPE Handbook.

And the candle example revisited:

Fig. 5.13 Reaction regions in a candle. Source: SFPE Handbook.