fdsreader Module#
In order to analyse simulation data computed by FDS with Python, we have developed the Python module fdsreader. Its aim is to read most data output formats generated by FDS and map them to Python data structures.
It is freely available and open source. The source code is hosted at GitHub: FireDynamics/fdsreader and there is also an API documentation.
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (6, 4)
import numpy as np
from IPython.display import display
from PIL import Image
Installation#
The fdsreader module can be installed via pip (see also the GitHub repository):
pip install fdsreader
However, it is already installed on all JupyterLab instances used for this lecture.
Basic Demo Data Set#
To demonstrate the usage of the fdsreader module, a simple FDS scenario (Steckler compartment) is utilized. Here, only a single mesh is used and only the fundamental data types are involved.
Full FDS input file
&HEAD CHID='StecklerExample', TITLE='Example of a Steckler case, with 3/6 door' /
&TIME T_END=1800.0 /
&DUMP NFRAMES=1800 /
&MISC BNDF_DEFAULT=F /
# ---------------------------------------
# Computational domain
# ---------------------------------------
&MESH ID = 'Domain_Simple',
IJK = 40,28,22,
XB = -1.40,2.60,-1.40,1.40,0.00,2.20 /
# ---------------------------------------
# Open boundary conditions
# ---------------------------------------
&VENT MB='XMAX', SURF_ID='OPEN' /
&VENT ID = 'OpenCeiling',
SURF_ID = 'OPEN',
XB = 1.51,2.60,-1.40,1.40,2.20,2.20 /
&VENT ID = 'OpenLeft',
SURF_ID = 'OPEN',
XB = 1.51,2.60,-1.40,-1.40,0.00,2.20 /
&VENT ID = 'OpenRight',
SURF_ID = 'OPEN',
XB = 1.51,2.60,1.40,1.40,0.00,2.20 /
# ---------------------------------------
# Gas burner: propane
# ---------------------------------------
&SPEC ID = 'PROPANE' /
&REAC FUEL = 'PROPANE',
SOOT_YIELD = 0.022 /
# HRR: 62.9 kW
&SURF ID = 'BURNER',
HRRPUA = 393.74999999999994,
SPEC_ID(1) = 'PROPANE'
COLOR = 'RASPBERRY' /
&OBST SURF_ID = 'INERT',
XB = -0.2, 0.2, -0.2, 0.2, 0.0, 0.2 /
&VENT SURF_ID = 'BURNER',
XB = -0.2, 0.2, -0.2, 0.2, 0.2, 0.2 /
# ---------------------------------------
# Surface definition (boundary conditions)
# ---------------------------------------
&SURF ID = 'Wall Lining',
COLOR = 'BEIGE',
DEFAULT = T,
THICKNESS(1:1) = 0.0254,
MATL_ID(1,1:1) = 'MARINITE',
MATL_MASS_FRACTION(1,1) = 1.0 /
&MATL ID = 'MARINITE'
EMISSIVITY = 0.9
DENSITY = 737.
SPECIFIC_HEAT = 1.2
CONDUCTIVITY = 0.12 /
# ---------------------------------------
# Geometrical Structure
# ---------------------------------------
&OBST ID = 'Ceiling',
SURF_ID = 'Wall Lining',
BNDF_OBST = T,
XB = -1.51,1.51,-1.51,1.51,2.20,2.31 /
&OBST ID = 'WallFront',
SURF_ID = 'Wall Lining'
XB = 1.40,1.51,-1.51,1.51,0.00,2.20 /
&OBST ID = 'WallRight',
SURF_ID = 'Wall Lining',
BNDF_OBST = T,
XB = -1.40,1.40,1.40,1.51,0.00,2.20 /
# Cut out for door
&HOLE ID = 'WallFront.001'
XB=1.4050,1.5150,-0.2000,0.2000,0.0000,1.8000 /
# ---------------------------------------
# Analytics
# ---------------------------------------
&SLCF PBX = 0.00
QUANTITY = 'TEMPERATURE' /
&SLCF PBY = 0.00
QUANTITY = 'TEMPERATURE' /
&SLCF PBX = 0.00
QUANTITY = 'W-VELOCITY' /
&SLCF PBY = 0.00
QUANTITY = 'U-VELOCITY' /
&SLCF PBZ = 1.80
QUANTITY = 'W-VELOCITY' /
&BNDF QUANTITY = 'WALL TEMPERATURE',
CELL_CENTERED = T /
&DEVC ID = 'Temp_Door_Low',
QUANTITY = 'TEMPERATURE',
XYZ = 1.45, 0.05, 0.1 /
&DEVC ID = 'Temp_Door_Mid',
QUANTITY = 'TEMPERATURE',
XYZ = 1.45, 0.05, 1.0 /
&DEVC ID = 'Temp_Door_High',
QUANTITY = 'TEMPERATURE',
XYZ = 1.45, 0.05, 1.65 /
&TAIL/
Precomputed simulation data
Open the Data Set#
First the fdsreader module needs to be loaded:
import fdsreader
The version of (any) module can be checked with the __version__ variable:
fdsreader.__version__
'1.9.1'
Next, the reader needs to be pointed to the directory, which contains the simulation data, especailly the smokeview file.
# define the path to the data
path_to_data = 'data/fdsreader/example_01/rundir'
sim = fdsreader.Simulation(path_to_data)
The Simulation object sim contains now all the information and data about the simulaiton output:
sim
Simulation(chid=StecklerExample,
meshes=1,
obstructions=4,
slices=5,
smoke_3d=3,
devices=4)
The variable sim contains information about the mesh (MESH), four slices (SLCF) and four point measurements (DEVC). The additional device – there were just three defined in the FDS input file – is the time column.
Tip
You can use the autocomplete function in Jupyter. This way you can quickly see available data structures and functions, especially in complex data types as the Simulation object.
Device Data#
The simplest data set is the output of the DEVC directives. The available data and meta information can be directly printed:
# short reference for convinience, i.e. `devc` contains all devices
devc = sim.devices
print(devc)
[Device(id='Time', xyz=(0.0, 0.0, 0.0), quantity=Quantity('TIME')),
Device(id='Temp_Door_Low', xyz=(1.45, 0.05, 0.1), quantity=Quantity('TEMPERATURE')),
Device(id='Temp_Door_Mid', xyz=(1.45, 0.05, 1.0), quantity=Quantity('TEMPERATURE')),
Device(id='Temp_Door_High', xyz=(1.45, 0.05, 1.65), quantity=Quantity('TEMPERATURE'))]
The Device class contains all relevant information, see device documentation.
for i in devc:
print(f"ID: {i.id},\t quantity: {i.quantity_name}, \t position: {i.position}")
ID: Time, quantity: TIME, position: (0.0, 0.0, 0.0)
ID: Temp_Door_Low, quantity: TEMPERATURE, position: (1.45, 0.05, 0.1)
ID: Temp_Door_Mid, quantity: TEMPERATURE, position: (1.45, 0.05, 1.0)
ID: Temp_Door_High, quantity: TEMPERATURE, position: (1.45, 0.05, 1.65)
Tip
Autocomplete works also for the dictionary keys ;-)
Individual devices, including the time column, are accessable as dictironary entries using their ID as key. The data of each individual device (Device.data) is stored as a numpy array:
type(devc['Temp_Door_Mid'].data)
numpy.ndarray
The length matches the expected value, i.e. 1801, as the simulation time was \(\mf 1800\ s\) and the divices were writen out every second, including the initial time step, here at \(\mf t=0\ s\).
len(devc['Time'].data)
1801
A raw look at the data (Device.data):
devc['Temp_Door_Mid'].data
array([ 20. , 20.002083, 20.034418, ..., 105.32822 , 114.82179 ,
115.01705 ], dtype=float32)
The device data can be also visualised with matplotlib:
# create the plot
plt.plot(devc['Time'].data, devc['Temp_Door_High'].data)
# label the axes
plt.xlabel("time / s")
devc_id = devc['Temp_Door_High'].id
devc_q = devc['Temp_Door_High'].quantity_name
devc_u = devc['Temp_Door_High'].unit
plt.ylabel(f"{devc_q} ({devc_id}) / {devc_u}")
# add a grid
plt.grid()
# save output to file
plt.savefig('figs/device_demo_01.svg', bbox_inches='tight')
plt.close()
Fig. 38 Visualization of the data of one of the devices.#
In the same manner a set of devices can be plotted at once. Like all devices with names starting with Temp_:
# loop over all devices
for i in devc:
# consider only devices with an ID that starts with 'Temp_'
if not i.id.startswith('Temp_'):
continue
plt.plot(devc["Time"].data, i.data, label=i.id)
plt.legend()
plt.xlabel("time / s")
plt.ylabel('temperature / $^\circ$C')
plt.grid()
# save output to file
plt.savefig('figs/device_demo_02.svg', bbox_inches='tight')
plt.close()
Fig. 39 Visualization of the data of a set of devices.#
HRR Data#
In the same fashion as the DEVC data, the data written to the HRR file can be directly accessed. It is not stored in the devices but in the hrr element of the Simulation object.
plt.plot(sim.hrr['Time'], sim.hrr['HRR'], label='heat release from fire')
plt.plot(sim.hrr['Time'], sim.hrr['Q_RADI'], label='radiative')
plt.plot(sim.hrr['Time'], sim.hrr['Q_COND'], label='conductive')
plt.plot(sim.hrr['Time'], sim.hrr['Q_CONV'], label='convective')
plt.plot(sim.hrr['Time'],
sim.hrr['HRR'] + sim.hrr['Q_RADI'] + sim.hrr['Q_COND'] + sim.hrr['Q_CONV'],
color='grey', label='sum', zorder=0)
plt.xlabel('time / s')
plt.ylabel('heat flow rate / kW')
plt.legend()
plt.grid()
# save output to file
plt.savefig('figs/hrr_demo_01.svg', bbox_inches='tight')
plt.close()
Fig. 40 Visualization of a set of columns from the HHR file.#
Slice Data#
Data generated by SLCF directives span over two or three spatial dimensions plus the time dimension. Besides that, they can be distributed across multiple meshes.
The data of a slice is stored for each mesh individually. In this simple example, there is only a single mesh, yet for formal consistency it still needs to be referred.
The data sturcutre is as follows
sim.slices[sliceid][meshid].data[timestep, direction1, direction2]
where sliceid is just the index of the slice, meshid is the index of the mesh, here in this example 0, and the reference to the data is given by the time step id and then the two spatial indices (for two dimensional slices).
In general there are multiple slice objects available:
# print available slice data
for slice in sim.slices:
print(f"Slice Type [2D/3D]: {slice.type}\n Quantity: {slice.quantity.name}\n",
f" Physical Extent: {slice.extent}\n Orientation [1/2/3]: {slice.orientation}\n")
Slice Type [2D/3D]: 2D
Quantity: TEMPERATURE
Physical Extent: Extent([0.00, 0.00] x [-1.40, 1.40] x [0.00, 2.20])
Orientation [1/2/3]: 1
Slice Type [2D/3D]: 2D
Quantity: TEMPERATURE
Physical Extent: Extent([-1.40, 2.60] x [0.00, 0.00] x [0.00, 2.20])
Orientation [1/2/3]: 2
Slice Type [2D/3D]: 2D
Quantity: W-VELOCITY
Physical Extent: Extent([0.00, 0.00] x [-1.40, 1.40] x [0.00, 2.20])
Orientation [1/2/3]: 1
Slice Type [2D/3D]: 2D
Quantity: U-VELOCITY
Physical Extent: Extent([-1.40, 2.60] x [0.00, 0.00] x [0.00, 2.20])
Orientation [1/2/3]: 2
Slice Type [2D/3D]: 2D
Quantity: W-VELOCITY
Physical Extent: Extent([-1.40, 2.60] x [-1.40, 1.40] x [1.80, 1.80])
Orientation [1/2/3]: 3
There are multiple ways to find the right slice in the set of all slices. One way is to filter for a quantity using the filter_by_quantity function or choose a slice by its ID.
# get the W-VELOCITY slice(s)
w_slice = sim.slices.filter_by_quantity("W-VELOCITY")
print(w_slice)
SliceCollection([Slice([2D] quantity=Quantity('W-VELOCITY'), cell_centered=False, extent=Extent([0.00, 0.00] x [-1.40, 1.40] x [0.00, 2.20]), extent_dirs=('y', 'z'), orientation=1),
Slice([2D] quantity=Quantity('W-VELOCITY'), cell_centered=False, extent=Extent([-1.40, 2.60] x [-1.40, 1.40] x [1.80, 1.80]), extent_dirs=('x', 'y'), orientation=3)])
Another way is to select a slice based on its distance to a given point.
# select slice, by its distance to a given point
slc = w_slice.get_nearest(x=1, z=2)
print(slc)
Slice([2D] quantity=Quantity('W-VELOCITY'), cell_centered=False, extent=Extent([-1.40, 2.60] x [-1.40, 1.40] x [1.80, 1.80]), extent_dirs=('x', 'y'), orientation=3)
To access the actual slice data, the actual mesh and a point in time needs to be specified. In this example, there is only one mesh, thus the index is 0. The function get_nearest_timestemp helps to find the right time index.
# choose and output the time step, next to t=75 s
it = slc.get_nearest_timestep(25)
print(f"Time step: {it}")
print(f"Simulation time: {slc.times[it]}")
Time step: 25
Simulation time: 25.02111
The following example illustrates the visualisation of the data and steps needed to adjust the representation. The needed adjustments are due to the data orientation expected by the imshow function.
# choose the temperature slice in y-direction
slc = sim.slices.filter_by_quantity('TEMPERATURE').get_nearest(x=3, y=0)
print(slc)
# only one mesh
slc_data = slc[0].data
print(slc_data)
Slice([2D] quantity=Quantity('TEMPERATURE'), cell_centered=False, extent=Extent([-1.40, 2.60] x [0.00, 0.00] x [0.00, 2.20]), extent_dirs=('x', 'z'), orientation=2)
[[[ 20. 20. 20. ... 20. 20. 20. ]
[ 20. 20. 20. ... 20. 20. 20. ]
[ 20. 20. 20. ... 20. 20. 20. ]
...
[ 20. 20. 20. ... 20. 20. 20. ]
[ 20. 20. 20. ... 20. 20. 20. ]
[ 20. 20. 20. ... 20. 20. 20. ]]
[[ 20.030926 20.031328 20.032204 ... 20.001385 20.001268 20.00117 ]
[ 20.030703 20.031597 20.033634 ... 20.001493 20.001345 20.001238]
[ 20.031723 20.033785 20.038801 ... 20.001757 20.001535 20.001389]
...
[ 20.006077 20.004908 20.002953 ... 20.001383 20.001154 20.00104 ]
[ 20.005085 20.004053 20.00236 ... 20.00129 20.001116 20.001026]
[ 20.004608 20.003656 20.0021 ... 20.00125 20.001104 20.001026]]
[[ 20.12404 20.126698 20.133305 ... 20.026028 20.02525 20.025595]
[ 20.116137 20.11882 20.12633 ... 20.02626 20.025606 20.02608 ]
[ 20.114033 20.117645 20.128752 ... 20.02802 20.027351 20.027908]
...
[ 20.018784 20.016739 20.013128 ... 20.00563 20.004776 20.004353]
[ 20.015898 20.014067 20.010876 ... 20.005054 20.004427 20.004118]
[ 20.01441 20.012737 20.00983 ... 20.004791 20.004278 20.00403 ]]
...
[[ 44.00391 43.917053 43.920734 ... 143.89009 142.69537 142.16621 ]
[ 44.004223 43.863914 43.708996 ... 143.29715 142.09953 141.6622 ]
[ 43.81018 43.64982 43.4085 ... 142.64955 141.90448 141.75969 ]
...
[ 20.284891 20.19156 20.076902 ... 90.631195 78.81051 72.00585 ]
[ 20.218634 20.140545 20.047134 ... 56.04536 43.176456 39.645744]
[ 20.151264 20.09307 20.028439 ... 34.67456 27.534237 27.970665]]
[[ 45.228874 45.115242 44.938766 ... 150.18481 150.12732 149.83371 ]
[ 44.492287 44.350613 44.180614 ... 149.79759 150.0778 149.77635 ]
[ 43.646873 43.590538 43.562504 ... 147.7298 148.82109 149.29768 ]
...
[ 20.281096 20.186028 20.071451 ... 106.69953 93.09295 83.79199 ]
[ 20.205025 20.13359 20.046276 ... 80.62758 71.11945 62.30358 ]
[ 20.16152 20.102564 20.033293 ... 65.56552 56.724525 46.839134]]
[[ 42.762764 42.892406 42.67096 ... 146.0912 145.20709 144.58104 ]
[ 43.14627 43.263447 43.141045 ... 145.02187 144.6713 143.69063 ]
[ 43.753468 43.769325 43.798447 ... 141.0417 142.32797 141.77148 ]
...
[ 20.268656 20.194078 20.08938 ... 72.89162 70.64532 65.348694]
[ 20.206676 20.136755 20.052374 ... 59.554634 49.809177 42.573883]
[ 20.180956 20.111738 20.035168 ... 48.16472 36.145966 31.134487]]]
# Initial visualasation of the data at time t=50 s
it = slc.get_nearest_timestep(50)
plt.imshow(slc_data[it]);
# save output to file
plt.savefig('figs/slice_imshow_01.svg', bbox_inches='tight')
plt.close()
Fig. 41 Visualization of a slice.#
# Access the transpose data using ndarray.T and set the origin of the output
plt.imshow(slc_data[it].T, origin='lower');
# save output to file
plt.savefig('figs/slice_imshow_02.svg', bbox_inches='tight')
plt.close()
Fig. 42 Visualization of a slice.#
# Finally, also the extend is specified to move from index to physical space
# Additionally, the maximal value is set using the vmax argument
plt.imshow(slc_data[it].T,
origin='lower',
vmax=200,
extent=slc.extent.as_list())
plt.colorbar(label='temperature / C', orientation='horizontal');
plt.xlabel('x coordinate / m')
plt.ylabel('z coordinate / m')
# save output to file
plt.savefig('figs/slice_imshow_03.svg', bbox_inches='tight')
plt.close()
Fig. 43 Visualization of a slice.#
Obstructions can be visualised using masks, i.e. the data points which lie inside an obstacle will be marked non-valid as an not-a-number (nan) value.
# Example for a multi plot
list_t = [0, 50, 100, 200, 300, 400]
fig, axs = plt.subplots(2,3, sharex=True, sharey=True)
for i in range(len(list_t)):
it = slc.get_nearest_timestep(list_t[i])
axs.flat[i].imshow(slc_data[it].T,
vmin=20,
vmax=400,
origin='lower',
extent=slc.extent.as_list())
axs.flat[i].set_title(f"t={slc.times[it]:.1f}")
# save output to file
plt.savefig('figs/slice_imshow_04.svg', bbox_inches='tight')
plt.close()
Fig. 44 Visualization of a slice.#
# Example for a plot of all slice quantities at a given point in time
it = sim.slices[0].get_nearest_timestep(100)
fig_count=0
for slc in sim.slices:
plt.imshow(slc[0].data[it].T,
origin='lower',
extent=slc.extent.as_list())
q = slc.quantity.quantity
u = slc.quantity.unit
plt.xlabel(f'{slc.extent_dirs[0]} / m')
plt.ylabel(f'{slc.extent_dirs[1]} / m')
plt.colorbar(label=f"{q} / {u}")
# save output to file
plt.savefig(f'figs/slice_multi_{fig_count:02d}.svg', bbox_inches='tight')
fig_count += 1
plt.close()
Fig. 45 Visualization of a slice.#
Fig. 46 Visualization of a slice.#
Fig. 47 Visualization of a slice.#
Fig. 48 Visualization of a slice.#
Fig. 49 Visualization of a slice.#
Advanced Demo#
In contrast to the above example, the computational domain is split into two meshes.
Full FDS input file
&HEAD CHID='StecklerExample', TITLE='Example of a Steckler case, with 3/6 door' /
&TIME T_END=1800.0 /
&DUMP NFRAMES=1800 /
&MISC BNDF_DEFAULT=F /
# ---------------------------------------
# Computational domain
# ---------------------------------------
&MESH ID = 'Domain_A',
IJK = 20,28,22,
XB = -1.40,0.60,-1.40,1.40,0.00,2.20 /
&MESH ID = 'Domain_B',
IJK = 20,28,22,
XB = 0.60,2.60,-1.40,1.40,0.00,2.20 /
# ---------------------------------------
# Open boundary conditions
# ---------------------------------------
&VENT MB='XMAX', SURF_ID='OPEN' /
&VENT ID = 'OpenCeiling',
SURF_ID = 'OPEN',
XB = 1.51,2.60,-1.40,1.40,2.20,2.20 /
&VENT ID = 'OpenLeft',
SURF_ID = 'OPEN',
XB = 1.51,2.60,-1.40,-1.40,0.00,2.20 /
&VENT ID = 'OpenRight',
SURF_ID = 'OPEN',
XB = 1.51,2.60,1.40,1.40,0.00,2.20 /
# ---------------------------------------
# Gas burner: propane
# ---------------------------------------
&SPEC ID = 'PROPANE' /
&REAC FUEL = 'PROPANE',
SOOT_YIELD = 0.022 /
# HRR: 62.9 kW
&SURF ID = 'BURNER',
HRRPUA = 393.74999999999994,
SPEC_ID(1) = 'PROPANE'
COLOR = 'RASPBERRY' /
&OBST SURF_ID = 'INERT',
XB = -0.2, 0.2, -0.2, 0.2, 0.0, 0.2 /
&VENT SURF_ID = 'BURNER',
XB = -0.2, 0.2, -0.2, 0.2, 0.2, 0.2 /
# ---------------------------------------
# Surface definition (boundary conditions)
# ---------------------------------------
&SURF ID = 'Wall Lining',
COLOR = 'BEIGE',
DEFAULT = T,
THICKNESS(1:1) = 0.0254,
MATL_ID(1,1:1) = 'MARINITE',
MATL_MASS_FRACTION(1,1) = 1.0 /
&MATL ID = 'MARINITE'
EMISSIVITY = 0.9
DENSITY = 737.
SPECIFIC_HEAT = 1.2
CONDUCTIVITY = 0.12 /
# ---------------------------------------
# Geometrical Structure
# ---------------------------------------
&OBST ID = 'Ceiling',
SURF_ID = 'Wall Lining',
BNDF_OBST = T,
XB = -1.51,1.51,-1.51,1.51,2.20,2.31 /
&OBST ID = 'WallFront',
SURF_ID = 'Wall Lining'
XB = 1.40,1.51,-1.51,1.51,0.00,2.20 /
&OBST ID = 'WallRight',
SURF_ID = 'Wall Lining',
BNDF_OBST = T,
XB = -1.40,1.40,1.40,1.51,0.00,2.20 /
# Cut out for door
&HOLE ID = 'WallFront.001'
XB=1.4050,1.5150,-0.2000,0.2000,0.0000,1.8000 /
# ---------------------------------------
# Analytics
# ---------------------------------------
&SLCF PBX = 0.00
QUANTITY = 'TEMPERATURE' /
&SLCF PBY = 0.00
QUANTITY = 'TEMPERATURE' /
&SLCF PBX = 0.00
QUANTITY = 'W-VELOCITY' /
&SLCF PBY = 0.00
QUANTITY = 'U-VELOCITY' /
&SLCF PBZ = 1.80
QUANTITY = 'W-VELOCITY' /
&BNDF QUANTITY = 'WALL TEMPERATURE',
CELL_CENTERED = T /
&DEVC ID = 'Temp_Door_Low',
QUANTITY = 'TEMPERATURE',
XYZ = 1.45, 0.05, 0.1 /
&DEVC ID = 'Temp_Door_Mid',
QUANTITY = 'TEMPERATURE',
XYZ = 1.45, 0.05, 1.0 /
&DEVC ID = 'Temp_Door_High',
QUANTITY = 'TEMPERATURE',
XYZ = 1.45, 0.05, 1.65 /
&TAIL/
Precomputed simulation data
# define the path to the data
path_to_data = 'data/fdsreader/example_02/rundir'
sim = fdsreader.Simulation(path_to_data)
print(sim)
Simulation(chid=StecklerExample,
meshes=2,
obstructions=4,
slices=5,
smoke_3d=3,
devices=4)
Multi Mesh Slices#
First, one of the slices is selected, e.g. the temperature slice normal to y
slc = sim.slices.filter_by_quantity('TEMPERATURE').get_nearest(x=2, y=0)
print(slc)
Slice([2D] quantity=Quantity('TEMPERATURE'), cell_centered=False, extent=Extent([-1.40, 2.60] x [0.00, 0.00] x [0.00, 2.20]), extent_dirs=('x', 'z'), orientation=2)
Each slice records in which meshes it is present. In this case, these are just two.
slc.meshes
[Mesh(id="Domain_A", extent=Extent([-1.40, 0.60] x [-1.40, 1.40] x [0.00, 2.20]), dimension=Dimension(21, 29, 23)),
Mesh(id="Domain_B", extent=Extent([0.60, 2.60] x [-1.40, 1.40] x [0.00, 2.20]), dimension=Dimension(21, 29, 23))]
The data strucutre of a slice is, that it consists of a set of sub-slices, one for each mesh. These are of variable size, depending on the mesh structure. The sub-slices can be individually accessed.
for m in slc.meshes:
print(slc.get_subslice(m))
SubSlice(shape=(21, 23), mesh=Domain_A, extent=Extent([-1.40, 0.60] x [0.00, 0.00] x [0.00, 2.20]))
SubSlice(shape=(21, 23), mesh=Domain_B, extent=Extent([0.60, 2.60] x [0.00, 0.00] x [0.00, 2.20]))
it = slc.get_nearest_timestep(100)
fig, axs = plt.subplots(1,2)
ax_count=0
for m in slc.meshes:
s = slc.get_subslice(m)
axs.flat[ax_count].imshow(s.data[it].T,
origin='lower',
extent=s.extent.as_list(),
vmax=200)
axs.flat[ax_count].set_xlabel(f'{slc.extent_dirs[0]} / m')
axs.flat[ax_count].set_ylabel(f'{slc.extent_dirs[1]} / m')
ax_count += 1
plt.tight_layout()
# save output to file
plt.savefig('figs/multi_slice_separate.svg', bbox_inches='tight')
plt.close()
Fig. 50 Individual visualization of slices on two meshes.#
In order to merge the subslices, the to_global function can be used.
gslice, gcoord = slc.to_global(return_coordinates=True)
print(type(gslice))
print(gslice.shape)
<class 'numpy.ndarray'>
(1801, 41, 23)
The resulting data structure can now be used the same way as the one mesh slices. Yet, the meta data needs to be drawn from the original slice object, as the result of to_global is a plain numpy array.
plt.imshow(gslice[it].T,
origin='lower',
extent=slc.extent.as_list(),
vmax=200)
plt.xlabel(f'{slc.extent_dirs[0]} / m')
plt.ylabel(f'{slc.extent_dirs[1]} / m')
plt.colorbar(orientation='horizontal', label=f'{slc.quantity.name} / {slc.quantity.unit}')
# save output to file
plt.savefig('figs/multi_slice_global.svg', bbox_inches='tight')
plt.close()
Fig. 51 Visualization of a global, i.e. merged, slice.#
Accessing Slice Data#
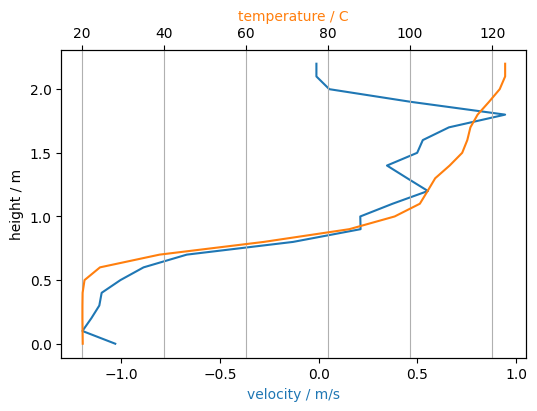
The data of a slice can be accessed to extract various subsets of data. For example, to create a temperature and x-velocity profile at a given time across the door (in z-direction) can be achieved with the following code.
# get the slice data as global objects
u_slice = sim.slices.filter_by_quantity('U-VELOCITY').get_nearest(x=2, y=0).to_global()
t_slice = sim.slices.filter_by_quantity('TEMPERATURE').get_nearest(x=2, y=0).to_global()
# define the time index
it = sim.slices[0].get_nearest_timestep(100)
fig, ax1 = plt.subplots()
ax2 = ax1.twiny()
# select spatial index (ix) based on physical position (x0)
x0 = 1.25
ix = np.where(gcoord['x'] >= x0)[0][0]
ax1.plot(u_slice[it][ix,:], gcoord['z'], label='x-velocity', color='C0')
ax2.plot(t_slice[it][ix,:], gcoord['z'], label='temperature', color='C1')
ax1.set_xlabel('velocity / m/s', color='C0')
ax2.set_xlabel('temperature / C', color='C1')
ax1.set_ylabel('height / m')
plt.grid()
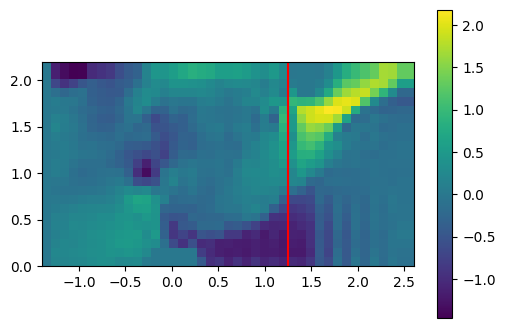
# illustrate the location of the extracted data
plt.imshow(u_slice[it].T,
origin='lower',
extent=slc.extent.as_list())
plt.axvline(x=x0, color='red')
plt.colorbar();
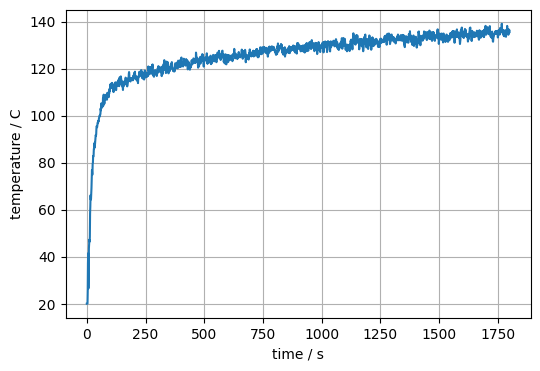
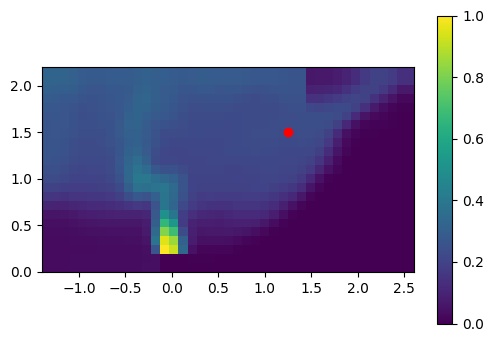
The time evolution of a quantity at a given location is accessed in a similar way.
# select spatial index
x0 = 1.25
z0 = 1.50
ix = np.where(gcoord['x'] >= x0)[0][0]
iy = np.where(gcoord['z'] >= z0)[0][0]
plt.plot(slc.times, t_slice[:, ix, iy])
plt.xlabel('time / s')
plt.ylabel('temperature / C')
plt.grid()
# illustrate the location of the extracted data
plt.imshow(t_slice[it].T,
origin='lower',
extent=slc.extent.as_list())
plt.scatter(x0, z0, color='red')
plt.colorbar();
Boundary Data#
In a similar manner as the slice data, the boudary data of obstructions can be accessed. As this data is bound to an obstruction in FDS, it is part of each individual obstruction object.
sim.obstructions
ObstructionCollection([Obstruction(id=1, Bounding-Box=Extent([-0.20, 0.20] x [-0.20, 0.20] x [0.00, 0.20]), SubObstructions=1),
Obstruction(id=2, Bounding-Box=Extent([-1.40, 1.51] x [-1.40, 1.40] x [2.20, 2.20]), SubObstructions=2, Quantities=['temp']),
Obstruction(id=4, Bounding-Box=Extent([-1.40, 1.40] x [1.40, 1.40] x [0.00, 2.20]), SubObstructions=2, Quantities=['temp']),
Obstruction(id=3, Bounding-Box=Extent([1.41, 1.51] x [-0.20, 0.20] x [0.00, 0.00]), SubObstructions=1)])
for o in sim.obstructions:
print(f'ID: {o.id}; has data: {o.has_boundary_data}')
if o.has_boundary_data:
print(f' orientations: {o.orientations}')
print(f' quantities: {o.quantities}')
print(f' number of involved meshes: {len(o.meshes)}')
ID: 1; has data: False
ID: 2; has data: True
orientations: [-3]
quantities: [Quantity('WALL TEMPERATURE')]
number of involved meshes: 2
ID: 4; has data: True
orientations: [-2]
quantities: [Quantity('WALL TEMPERATURE')]
number of involved meshes: 2
ID: 3; has data: False
Let’s select the boundary at the ceiling, i.e. the one with orientation -3.
obst = sim.obstructions.get_by_id(2)
print(obst)
Obstruction(id=2, Bounding-Box=Extent([-1.40, 1.51] x [-1.40, 1.40] x [2.20, 2.20]), SubObstructions=2, Quantities=['temp'])
The time step index and the global, due to multiple meshes involved, data structure. The function get_global_boundary_data_arrays needs the quantity and the orientation to create a numpy data object.
obst = sim.obstructions[1]
it = obst.get_nearest_timestep(100)
data = obst.get_global_boundary_data_arrays('WALL TEMPERATURE')[-3]
print(f'shape of the data object: {data.shape}')
shape of the data object: (1801, 29, 28)
plt.imshow(data[it].T,
origin='lower', extent=obst.bounding_box.as_list())
plt.colorbar()
<matplotlib.colorbar.Colorbar at 0x10ff42da0>
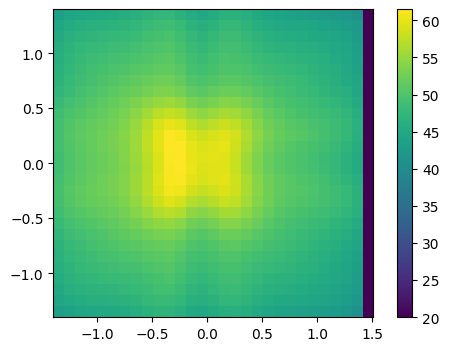
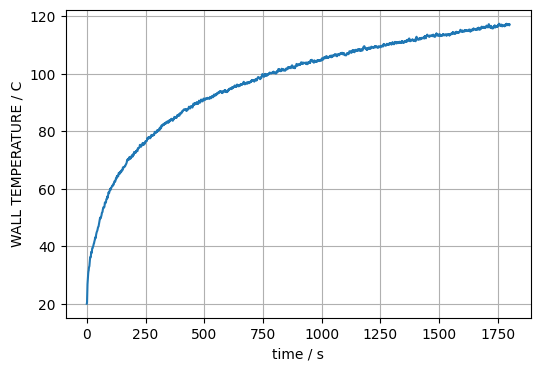
In the same mannor as above, e.g. time series at a given point on the boundary can be created. For a point at the center of the boundary, this could be something like this:
ix = data.shape[1] // 2
iy = data.shape[2] // 2
plt.plot(obst.times, data[:, ix, iy])
plt.xlabel('time / s')
plt.ylabel(f'{obst.quantities[0].name} / {obst.quantities[0].unit}')
plt.grid()