1.1. Zahlendarstellung#
In dieser Aufgabe wird die digitale Darstellung von ganzen und reellen Zahlen vertieft. Insbesondere soll die Umwandlung von reellen Zahlen in Gleitkommazahlen verdeutlicht und die Grenzen der digitalen Darstellung illustriert werden.
Grundlagen und Beispiele#
Ganze Zahlen#
Die Umwandlung ganzer Zahlen erfolt direkt über die Zahlendarstellung im Dualsystem. Soll ein Vorzeichen dargestellt werden, so wird dieses im höchsten Bit gespeichert. Hierbei wird oft die Zahl als negativ interpretiert, wenn das höchste Bit einen Wert von Eins hat.
Gleitkommazahlen#
Die Darstellung von Gleitkommzahlen in binären Systemen kann auf unterschiedliche Weisen erfolgen. Die mit Abstand weitverbreiteste Methode wird im IEEE754 Standard beschrieben. Die hier verwendeten Beispiele folgen dem Verfahren dieses Standards und werden im folgenden kurz vorgestellt.
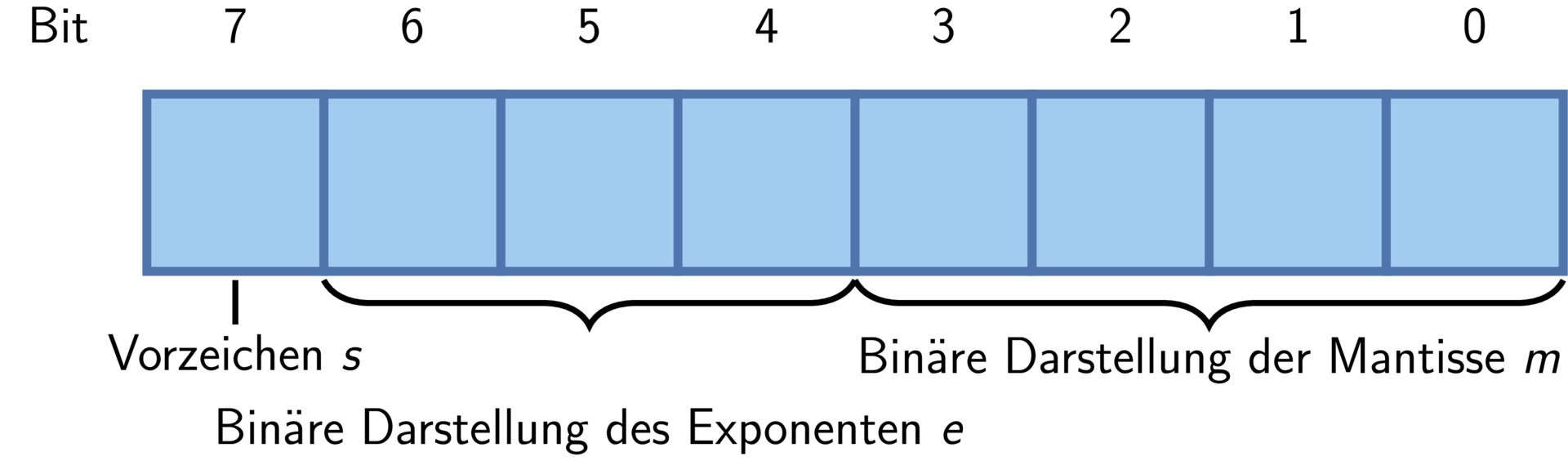
Für einen besseren Überblick und eine kürzere Schreibweise wird in diesem Beispiel eine hypothetische 8-Bit-Darstellung verwendet. Die real eingesetzten Verfahren für höhere Bitwerte, typischerweise 32 und 64 Bit, sind gleich. Eine mögliche Aufteilung der Bits könnte wie in folgender Abbildung aussehen.
|
|---|
Bild: Hypothetische Bitaufteilung einer 8-Bit Darstellung einer Gleitkommazahl |
In diesem Beispiel wird eine Gleitkommazahl \(a\) wie folgt durch das Vorzeichen \(s\), die Mantisse \(m\) umd den Exponenten \(e\) abgebildet: \(a = (-1)^{s} \cdot (1.0+m) \cdot 2^{e-3}\)
Zur Umwandlung von der binären Darstellung in eine Gleitkommazahl sind folgende Schritte notwendig. Diese werden anhand der Bitfolge 110110112 verdeutlicht.
Schritt 0#
Zur besseren visuellen Darstellung werden die Bitgruppen getrennt nach obiger Aufteilung dargestellt:
110110112 = 1 101 10112
Schritt 1#
Bestimmen Sie das Vorzeichen der Gleitkommazahl
Vorzeichenbit = 1 : die Gleitkommazahl ist negativ
Vorzeichenbit = 0 : die Gleitkommazahl ist positiv
In unserem Beispiel ist die Gleitkommazahl negativ.
Schritt 2#
Berechnen Sie den Exponenten \(e\) indem Sie die binäre Zahl in das Dezimalsystem umwandeln. Hierbei wird eine vorzeichenlose ganze Zahl angenommen.
In unserem Beispiel ergibt sich somit \(e\) = 1012 = 510
Schritt 3#
Als letztes muss noch die Mantisse bestimmt werden. Da durch die Mantisse keine ganze Zahl dargestellt werden soll, ist hier die Umwandlung etwas komplexer.
Um eine – in diesem Zahlenformat definierte – Umrechnung zu demonstrieren werden die Bits der Mantisse durchnummeriert. Von links nach rechts gehend, sind die einzelnen n-Bits der Mantisse wie folgt gekennzeichnet: \(m_1\), \(\dots\), \(m_n\). In unserem Beispiel ist \(n=4\) und
Bits der Mantisse: 10112
\(m_1 = 1\)
\(m_2 = 0\)
\(m_3 = 1\)
\(m_4 = 1\)
Der Formatdefinition wird der Wert der Mantisse \(m\) mit folgender Vorschrift berechnet:
Und somit ergibt sich folgender Wert für \(m\) in unserem Beispiel:
Schritt 4#
Werden nun alle obigen Schritte zusammengesetzt, so ergibt sich mit
für die Gleitkommazahl \(a\) folgender Wert
Aufgabenstellung#
Aufgabenteil A#
Wandeln Sie folgende Dezimalzahlen in Binärzahlen um. Beachten Sie dabei den gewünschten Datentyp.
Dezimalzahl |
digitales Format |
|---|---|
11110 |
8-Bit Darstellung ohne Vorzeichen |
-52210 |
16-Bit Darstellung mit Vorzeichen |
30010 |
16-Bit Darstellung ohne Vorzeichen |
-11210 |
8-Bit Darstellung mit Vorzeichen |
12810 |
8-Bit Darstellung mit Vorzeichen |
Lösungshinweis#
Die Anzahl der Einsen in der binären Darstellung für die ersten drei Zahlen sind: 6, 4, 4.
Lösungsvorschlag#
11110 = 0110 11112
-52210 = 1000 0010 0000 10102
30010 = 0000 0001 0010 11002
-11210 = 1111 00002
nicht möglich, da mit 7 Bit (eines ist für das Vorzeichen vorbehalten) die maximale Zahl 127 ist
Aufgabenteil B#
Wandeln Sie folgende binäre Gleitkommazahlen (8 Bit) in ihr dezimales Äquivalent um. Verwenden Sie die oben vorgestellte Umwandlung.
010101002
111000102
Welche Gleitkommazahl ist vom Betrag her die kleinste darstellbare Zahl in diesem Format? Hierzu ist es hilfreich zuerst die binäre Darstellung zu bestimmen.
Lösungshinweis#
Die beiden umzuwandelnden Zahlen liegen vom Betrag her zwischen 4 und 10. Schreibt man die Gleitkommazahl auf, so sind ab der zweiten Nachkommastelle alle Stellen gleich Null.
Lösungsvorschlag#
0 101 01002 = 5.0
1 110 00102 = -9.0
Aufgabenteil C#
Bestimmen Sie die binäre Darstellung im obigen hypothetischen 8-Bit-Format folgender Gleitkommazahlen:
1.0
0.5
1.5
und optional auch für diese Zahlen:
3.0
-2.5
Lösungshinweis#
Die Anzahl der Einsen in der binären Darstellung der oberen drei Zahlen ist: 2, 1, 3.
Lösungsvorschlag#
0 011 0000
0 010 0000
0 011 1000
und
0 100 1000
1 100 0100
Lösungsvorschlag#
Die Antwort auf diese Frage lautet: Es kommt darauf an. Hierbei ist es wichtig zu verstehen, dass Gleitkommazahlen, wie die 0.1, 0.2 oder auch 0.3 nicht exakt als Gleitkommazahl im Dualsystem dargestellt werden können. Konkret für diese Zahlen heisst das, dass bei der Umwandlung in eine binäre Gleitkommazahl
0.1 zu 0.10000000149,
0.2 zu 0.20000000298 und
0.3 zu 0.30000001192
angenäht werden. Hinweis: Nützlich für diese Betrachtung ist ein Gleitkommazahlkonverter, wie dieser Gleitkommazahlkonverter.
Addiert man nun die binären Repräsentationen von 0.1 und 0.2, ergibt das
Die Zahl 0.3000000045 kann binär nicht exakt abgebildet werden, sondern wird als 0.30000001192 abgespeichert. Das entspricht exakt der binären Darstellung von 0.3. Damit würde in diesem Fall die Addition von 0.1 und 0.2 in diesem Zahlenformat die 0.3 ergeben.
Das muss aber nicht immer so sein. Die Addition von 1.1 und 0.2 verdeutlicht dies. Die binären Darstellungen lauten:
0.2 wird binär zu 0.20000000298
1.1 wird zu 1.10000002384
Die Summe beider lautet
Allerdings ist dies keine darstellbare Zahl in diesem Format und wird zu 1.30000007153 umgewandelt. Dies entspricht aber nicht der Darstellung von 1.3, welche 1.29999995232 wäre. Das bedeutet, dass bei der Berechnung obiger Summe folgende Ausgabe zu erwarten wäre
Show code cell outputs
0.1 -> 0.10000000149
0.2 -> 0.20000000298
0.3 -> 0.30000001192
0.1+0.2 -> 0.30000001192
(0.1+0.2)-0.3 -> 0.00000000000
1.1 -> 1.10000002384
0.2 -> 0.20000000298
1.3 -> 1.29999995232
1.1+0.2 -> 1.30000007153
(1.1+0.2)-1.3 -> 0.00000011921