3.3.2. Fitting

import numpy as np
np.set_printoptions(precision=2, linewidth=65)

import matplotlib.pyplot as plt
plt.rc('figure', dpi=150)

import seaborn as sns
sns.set()
sns.set_style('ticks')
sns.set_context("notebook", font_scale=1.2, rc={"lines.linewidth": 1.2})

Beim Fitting wird eine Modellfunktion gesucht, weche die Messdaten nicht unbedingt exakt abbildet. Wird ein Polynom verwendet, so hat es eine Grad, welcher deutlich kleiner ist, als die Anzahl der Messpunkte. Lineare Regression ist ein Beispiel für ein Fitting durch ein Polynom mit dem Grad Eins.

Zum Fitten durch ein Polynom kann die Funktion np.polyfit verwendet werden, genauso wie bei der Polynominterpolation. Diesmal jedoch mit einem kleineren Polynomgrad.

Im folgenden Beispiel werden zunächst Modelldaten generiert und dann mit entsprechenden Polynomen gefittet.

xmin = 0
xmax = 5
x = np.linspace(xmin, xmax, 100)

ni = 25

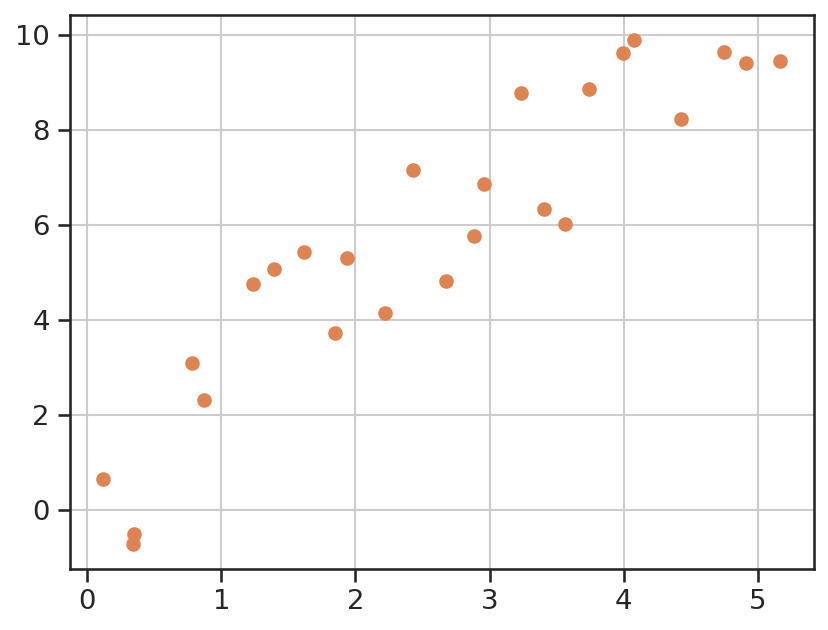
# x-Werte mit leichtem Rauschen
xi = np.linspace(xmin, xmax, ni) + 0.2*(2 * np.random.random(ni) -1)

# y(x) = 2x+0.5 mit leichtem Rauschen
yi = 2*xi + 0.5 + 2*(2 * np.random.random(ni) -1)

plt.scatter(xi, yi, color='C1')
plt.grid();

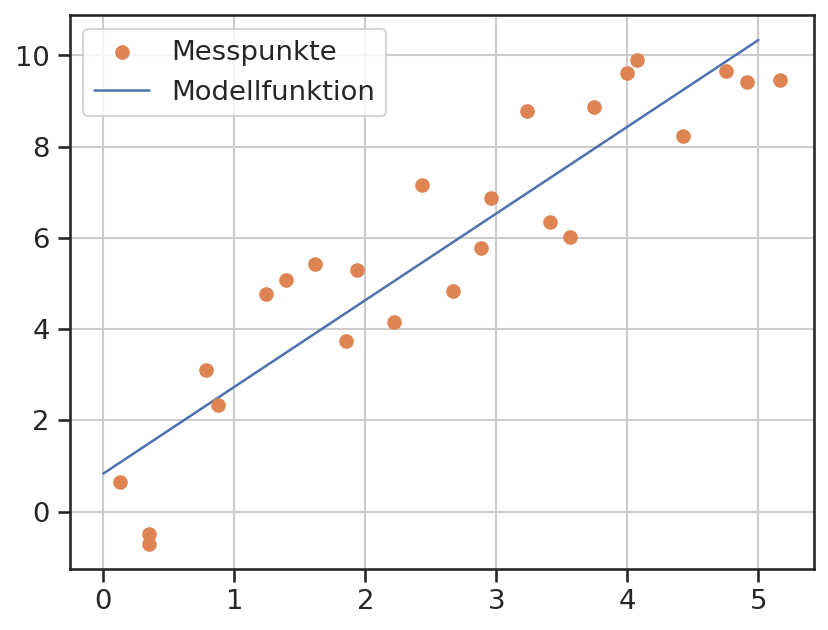
P1 = np.polyfit(xi, yi, 1)

plt.scatter(xi, yi, color='C1', zorder=3, label='Messpunkte')
plt.plot(x, np.polyval(P1, x), color='C0', label="Modellfunktion")
plt.grid()
plt.legend();

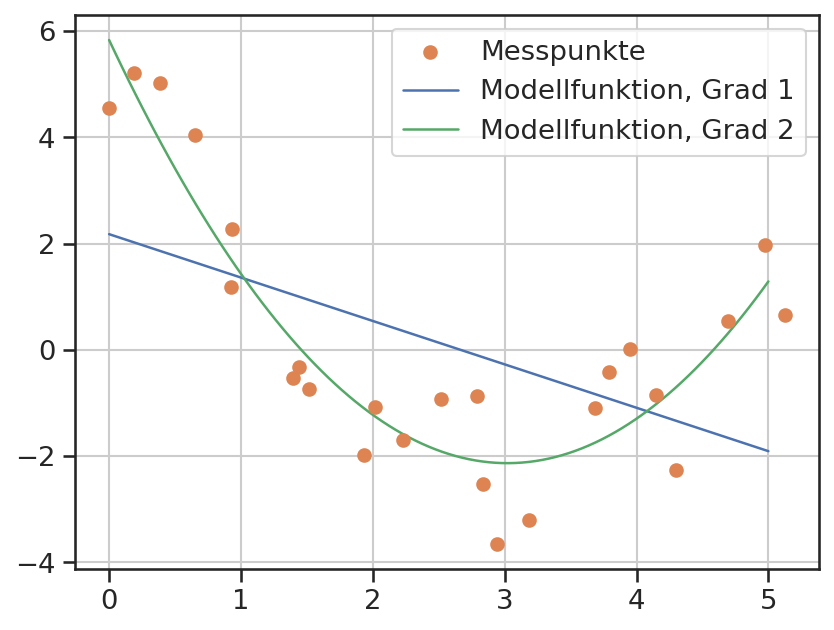
# x-Werte mit leichtem Rauschen
xi = np.linspace(xmin, xmax, ni) + 0.2*(2 * np.random.random(ni) -1)

# y(x) = 2x+0.5 mit leichtem Rauschen
yi = (xi - 2)**2 -2*xi + 2.5 + 2*(2 * np.random.random(ni) -1)

P1 = np.polyfit(xi, yi, 1)
P2 = np.polyfit(xi, yi, 2)

plt.scatter(xi, yi, color='C1', zorder=3, label='Messpunkte')
plt.plot(x, np.polyval(P1, x), color='C0', label="Modellfunktion, Grad 1")
plt.plot(x, np.polyval(P2, x), color='C2', label="Modellfunktion, Grad 2")
plt.grid()
plt.legend();