4.5. Ableitungsfunktion

In dieser Aufgabe wird die numerische Berechnung der Ableitungsfunktion vorgestellt. Insbesondere wird die Berechnung der Werte am Rand und der Berechnungsfehler betrachtet.

Aufgabenteil A

Gegeben ist die Funktion \(\sf y(x)\) mit

\[ \sf y(x) = e^{-(x-2)^2} \]

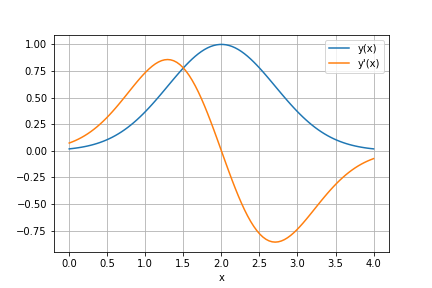
Stellen Sie die Funktion \(\sf y\) und deren Ableitung \(\sf y'\) graphisch im Intervall \(\sf x \in [0,4]\) dar.

Lösungshinweis

Die Ausgabe könnte wie folgt aussehen.

Lösungsvorschlag

Die analytische Ableitung der Funktion \(\sf y(x)\) lautet

\[ \sf y'(x) = - 2(x-2)e^{-(x-2)^2} \]

Show code cell content Hide code cell content

import numpy as np
import matplotlib.pyplot as plt

Show code cell content Hide code cell content

x = np.linspace(0, 4, 100)
y = np.exp(-(x-2)**2)
yp = -2*(x-2)*np.exp(-(x-2)**2)

Show code cell content Hide code cell content

plt.plot(x, y, label='y(x)')
plt.plot(x, yp, label='y\'(x)')

plt.legend()
plt.grid()
plt.xlabel('x')

# Ausgabe für den Lösungshinweis
# plt.savefig('teil1.png')

Text(0.5, 0, 'x')

Aufgabenteil B

Diskretisieren Sie die das obige Intervall, z.B. mit 20 Stützstellen, und bestimmen sie numerisch die Ableitungsfunktion. Für Stützstellen, welche nicht am Rand liegen, verwenden Sie die zentrale Differenzenformel zweiter Ordnung. Die Randwerte werden mit den Vorwärtsdifferenzenquotienten

\[ \sf y'_i = \frac{y_{i+1} - y_i}{\Delta x} \]

bzw. mit dem Rückwärtsdifferenzentquotienten

\[ \sf y'_i = \frac{y_{i} - y_{i-1}}{\Delta x} \]

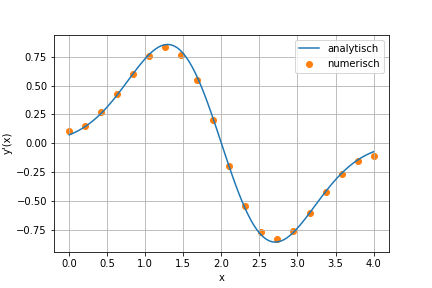
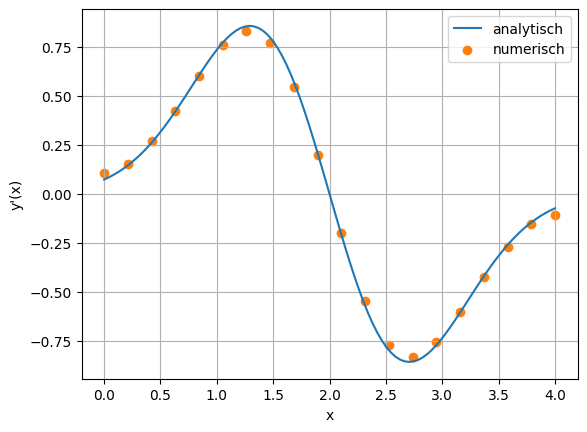
jeweils erster Ordnung berechnet. Stellen Sie die analytisch und numerisch bestimmten Ableitungsfunktionen zusammen dar.

Lösungshinweis

Die Ausgabe könnte wie folgt aussehen.

Lösungsvorschlag

Show code cell content Hide code cell content

# Definition der Anzahl der Stützstellen für die Diskretisierung
nx = 20

# Diskretisierung des betrachteten Intervalls
xi = np.linspace(0, 4, nx)
dx = xi[1] - xi[0]

# Funktionswerte an den Stützstellen xi
yi = np.exp(-(xi-2)**2)

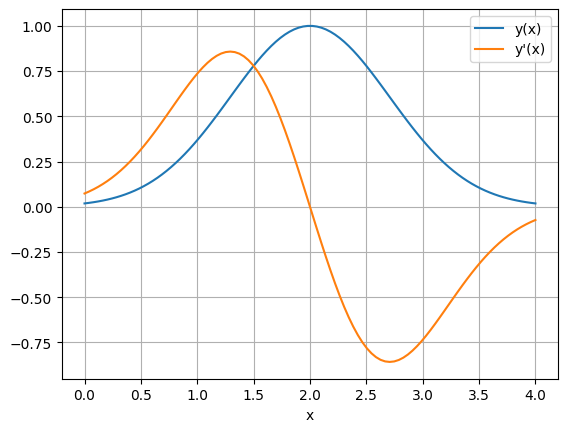
# Graphische Ausgabe, nur zur visuellen Kontrolle
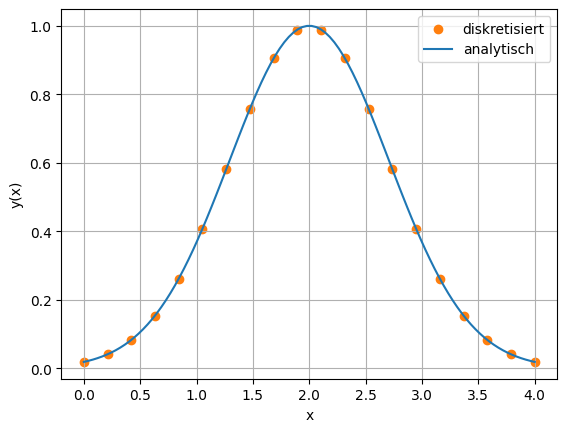
plt.scatter(xi, yi, c='C1', label='diskretisiert')
plt.plot(x, y, label='analytisch')

plt.xlabel('x')
plt.ylabel('y(x)')
plt.legend()
plt.grid();

Show code cell content Hide code cell content

# Erstellung eines Arrays für die numerische Ableitung
yip = np.zeros_like(yi)

# Berechnung der Ableitung im inneren Bereich, d.h.
# ohne die Randwerte, mit der zentralen Differenzenformel
yip[1:-1] = (yi[2:] - yi[:-2]) / (2*dx)

# Berechnung der Ableitung an den Randpunkten
# mit der Vorwärtsdifferenzenformel
yip[0] = (yi[1] - yi[0]) / dx
# mit der Rückwärtsdifferenzenformel
yip[-1] = (yi[-1] - yi[-2]) / dx

# yip[0] = (-3*yi[0] + 4*yi[1] - yi[2]) / (2*dx)
# yip[-1] = (3*yi[-1] - 4*yi[-2] + yi[-3]) / (2*dx)

# Graphische Ausgabe
plt.plot(x, yp, label='analytisch')
plt.scatter(xi, yip, c='C1', label='numerisch')

plt.legend()
plt.ylabel('y\'(x)')
plt.xlabel('x')
plt.grid()

# Ausgabe für den Lösungshinweis 
# plt.savefig('teil2.png')

Aufgabenteil C

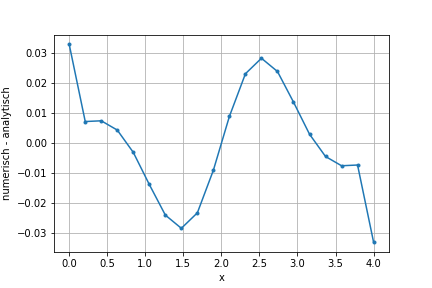
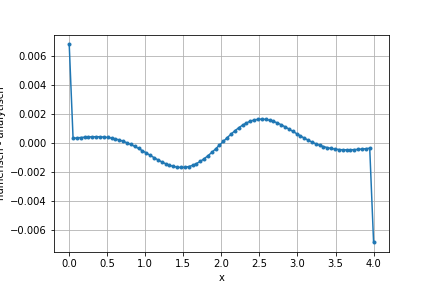
Berechnen Sie die Abweichung zwischen der analytischen und numerischen Ableitung an jedem Stützpunkt und stellen Sie diese graphisch dar. Verkleinern Sie den Gitterabstand \(\sf \Delta x\), z.B. um einen Faktor 4. Was fällt Ihnen auf?

Lösungshinweis

Die Ausgaben könnten wie folgt aussehen.

Lösungsvorschlag

Show code cell content Hide code cell content

# Definition einer Hilfsfunktion
def ableitung_f1(nx):
    # Diskretisierung des betrachteten Intervalls
    xi = np.linspace(0, 4, nx)
    dx = xi[1] - xi[0]

    # Funktionswerte an den Stützstellen xi
    yi = np.exp(-(xi-2)**2)
    
    # Erstellung eines Arrays für die numerische Ableitung
    yip = np.zeros_like(yi)

    # Berechnung der Ableitung im inneren Bereich, d.h.
    # ohne die Randwerte, mit der zentralen Differenzenformel
    yip[1:-1] = (yi[2:] - yi[:-2]) / (2*dx)

    # Berechnung der Ableitung an den Randpunkten
    # mit der Vorwärtsdifferenzenformel
    yip[0] = (yi[1] - yi[0]) / dx
    # mit der Rückwärtsdifferenzenformel
    yip[-1] = (yi[-1] - yi[-2]) / dx
    
    return xi, yip

Show code cell content Hide code cell content

# Analytische Ableitung als Funktion
def ableitung_analytisch(x):
    return -2*(x-2)*np.exp(-(x-2)**2)

Show code cell content Hide code cell content

# Ausgabe für den Lösungshinweis nx = 20
xi, yip = ableitung_f1(20)
yip_analytisch = ableitung_analytisch(xi)
    
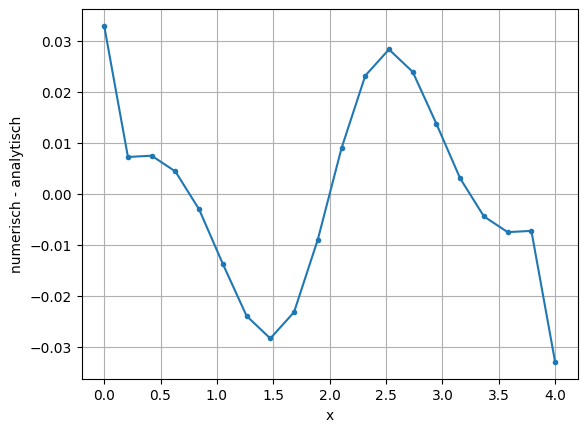
diff = yip - yip_analytisch
plt.plot(xi, diff, marker='.')
plt.grid()
plt.xlabel('x')
plt.ylabel('numerisch - analytisch')
# plt.savefig('teil3a.png')

Text(0, 0.5, 'numerisch - analytisch')

Show code cell content Hide code cell content

# Ausgabe für den Lösungshinweis nx = 80
xi, yip = ableitung_f1(80)
yip_analytisch = ableitung_analytisch(xi)
    
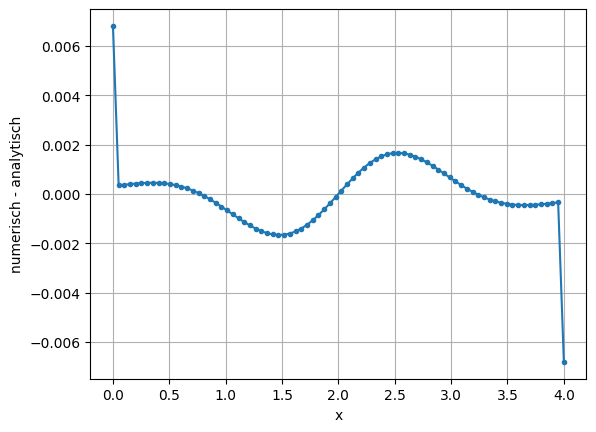
diff = yip - yip_analytisch
plt.plot(xi, diff, marker='.')
plt.grid()
plt.xlabel('x')
plt.ylabel('numerisch - analytisch')
# plt.savefig('teil3b.png')

Text(0, 0.5, 'numerisch - analytisch')

Show code cell content Hide code cell content

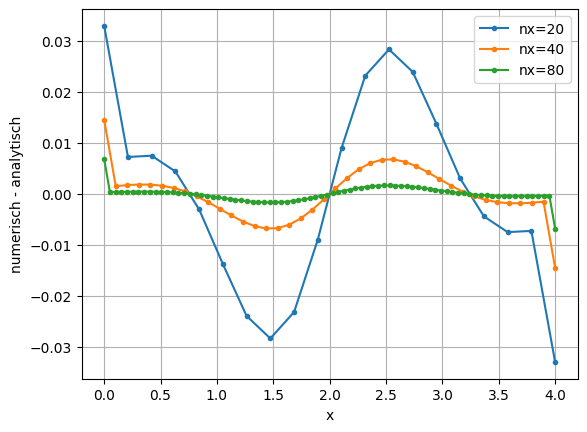
for nx in [20, 40, 80]:
    xi, yip = ableitung_f1(nx)
    yip_analytisch = ableitung_analytisch(xi)
    
    diff = yip - yip_analytisch
    plt.plot(xi, diff, marker='.', label=f'nx={nx}')

plt.legend()
plt.grid()
plt.xlabel('x')
plt.ylabel('numerisch - analytisch');

Aufgabenteil D

Bestimmen Sie die Formel für den Vorwärtsdifferenzenquotienten zweiter Ordnung zur Berechnung der ersten Ableitung. Verwenden Sie dafür die Taylor-Entwicklung an zwei vorwärtsgerichteten Punkten, d.h. \(\sf i+1, i+2\).

Die Rückwärtsformel lautet

\[ \sf y'_i = \frac{3y_{i} - 4y_{i-1} + y_{i-2}}{2\Delta x} + \mathcal{O}\left(\Delta x^2\right)\]

Lösungsvorschlag

Die Taylor-Entwicklungen an den Stellen \(\sf x_i + \Delta x = x_{i+1}\) bzw. \(\sf x_i + \Delta x = x_{i+1}\) lauten bis zur Ordnung \(\sf \mathcal{O}\left(\Delta x^3\right)\):

\[\sf y(x_i + \Delta x) = y_{i+1} = y_i + y'_i\Delta x + \frac{1}{2}y''_i\Delta x^2 + \mathcal{O}\left(\Delta x^3\right) \]

\[\sf y(x_i + 2\Delta x) = y_{i+2} = y_i + y'_i(2\Delta x) + \frac{1}{2}y''_i(2\Delta x)^2 + \mathcal{O}\left(\Delta x^3\right) \]

Das Ziel ist die Bestimmung des Terms \(\sf y'\) nur mit Hilfe von den Funktionswerten, d.h. \(\sf y\). Das bedeutet, dass die Terme der zweiten Ableitungen \(\sf y''\) eliminiert werden müssen. Dies kann errreicht werden indem die erste Gleichung mit vier multipliziert wird und dann die zweite Gleichung davon substrahiert wird.

\[\sf 4y_{i+1} = 4y_i + 4y'_i\Delta x + 2y''_i\Delta x^2 + \mathcal{O}\left(\Delta x^3\right) \]

\[\sf y_{i+2} = y_i + 2y'_i\Delta x + 2y''_i\Delta x^2 + \mathcal{O}\left(\Delta x^3\right) \]

\[\sf \Rightarrow 4y_{i+1} - y_{i+2} = 3y_i + 2y'_i\Delta x + \mathcal{O}\left(\Delta x^3\right) \]

Die Auflösung nach \(\sf y'_i\) führt zu

\[ \sf y'_i = \frac{-3y_i + 4y_{i+1} - y_{i+2}}{2\Delta x} + \mathcal{O}\left(\Delta x^2\right) \]

Dies ist die Vorwärtsdifferenzenformel für die erste Ableitung zweiter Ordnung.

Aufgabenteil E

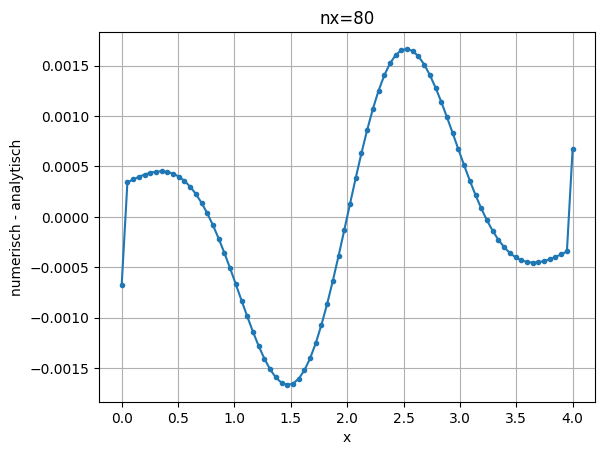
Verwenden Sie die Formeln zweiter Ordnung für die Berechnung der Ableitung am Rand. Wie sieht nun die Abweichung zwischen der analytischen und numerischen Ableitung aus?

Lösungshinweis

Die Ausgabe könnte wie folgt aussehen.

Lösungsvorschlag

Show code cell content Hide code cell content

# Definition einer Hilfsfunktion, jetzt mit der Randberechnung 
# zweiter Ordnung
def ableitung_f2(nx):
    # Diskretisierung des betrachteten Intervalls
    xi = np.linspace(0, 4, nx)
    dx = xi[1] - xi[0]

    # Funktionswerte an den Stützstellen xi
    yi = np.exp(-(xi-2)**2)
    
    # Erstellung eines Arrays für die numerische Ableitung
    yip = np.zeros_like(yi)

    # Berechnung der Ableitung im inneren Bereich, d.h.
    # ohne die Randwerte, mit der zentralen Differenzenformel
    yip[1:-1] = (yi[2:] - yi[:-2]) / (2*dx)

    # Berechnung der Ableitung an den Randpunkten
    # mit der Vorwärtsdifferenzenformel
    yip[0] = (-3*yi[0] + 4*yi[1] - yi[2]) / (2*dx)
    # mit der Rückwärtsdifferenzenformel
    yip[-1] = (3*yi[-1] - 4*yi[-2] + yi[-3]) / (2*dx)
    
    return xi, yip

Show code cell content Hide code cell content

# Ausgabe für den Lösungshinweis nx = 80
xi, yip = ableitung_f2(80)
yip_analytisch = ableitung_analytisch(xi)
    
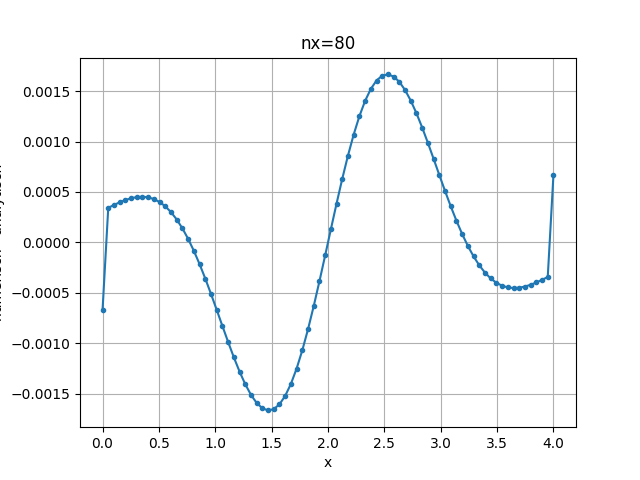
diff = yip - yip_analytisch
plt.plot(xi, diff, marker='.')
plt.grid()
plt.title('nx=80')
plt.xlabel('x')
plt.ylabel('numerisch - analytisch')
plt.savefig('teil5.png')

Show code cell content Hide code cell content

# Vergleichende Ausgabe
xi, yip_f1 = ableitung_f1(80)
xi, yip_f2 = ableitung_f2(80)

yip_analytisch = ableitung_analytisch(xi)
    
diff_f1 = yip_f1 - yip_analytisch
diff_f2 = yip_f2 - yip_analytisch

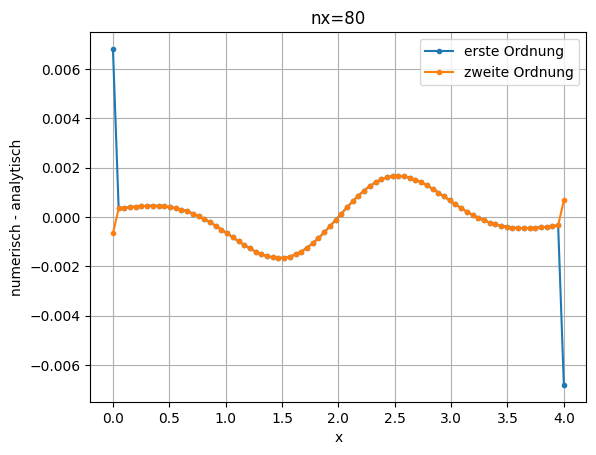
plt.plot(xi, diff_f1, marker='.', label='erste Ordnung')
plt.plot(xi, diff_f2, marker='.', label='zweite Ordnung')

plt.legend()
plt.grid()
plt.title('nx=80')
plt.xlabel('x')
plt.ylabel('numerisch - analytisch');