4.3.1. Finite-Differenzen-Methode

Show code cell source Hide code cell source

import numpy as np
np.set_printoptions(precision=2, linewidth=65)

import matplotlib.pyplot as plt
plt.rc('figure', dpi=150)

import seaborn as sns
sns.set()
sns.set_style('ticks')
sns.set_context("notebook", font_scale=1.2, rc={"lines.linewidth": 1.2})

Die Finite-Differenzen-Methode ist eine der einfachsten numerischen Verfahren zur Lösung von Differentialgleichungen. Die Grundidee ist die Ersetzung der Ableitungsoperationen durch Differenzenformeln. Die Lösung selbst wird auf einem diskretisierten Bereich gesucht.

Diskretisierung

Unter Diskretisierung wird die Aufteilung des Berechnungsbereichs in endlich viele Stützstellen verstanden. Diese haben im Allgemeinen den gleichen Abstand zueinander. Werden \(\sf n+1\) Stellen im Intervall \(\sf [a,b]\) gewählt, so ergibt sich damit folgende Nomenklatur für den Definitions- und Wertebereich

\[ \sf \Delta x = \frac{b-a}{n} \]

\[ \sf x_i = a + i\Delta x \quad \text{mit} \quad x_0 = a, \ x_n = b \]

\[ \sf f_i = f(x_i) = f(a+i\Delta x) \]

Dabei wird \(\sf \Delta x\) Gitterweite genannt.

# Anzahl der Stützstellen
n = 10

# Stützstellen
xi = np.linspace(0, 2, n)

# Gitterweite
dx = xi[1] - xi[0]

# Bsp. Funktionswerte an den Stützstellen
yi = np.sin(3*xi) + 2*xi

# für die Visualisierung der analytischen Funktion
x = np.linspace(0, 2, 100)
y = np.sin(3*x) + 2*x

# Darstellung der Daten
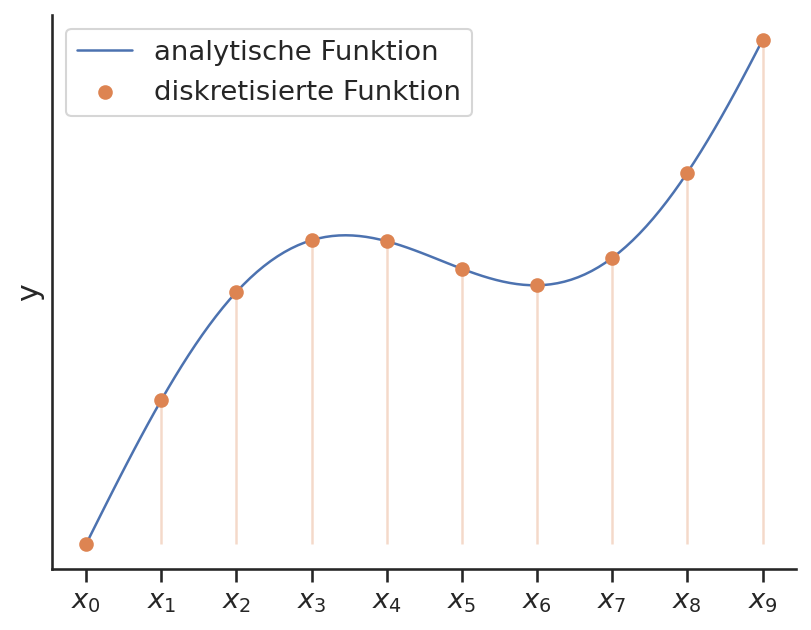
plt.plot(x, y, label='analytische Funktion')
plt.scatter(xi, yi, c='C1', label='diskretisierte Funktion', zorder=3)

# keine y-Achsen-Beschriftung
plt.yticks([])
plt.ylabel('y')

# angepasste x-Achsen-Beschriftung
ax = plt.gca()
ax.set_xticks(xi)
xlabels = []
for i in range(n):
    xlabels.append(f'$x_{i}$')
ax.set_xticklabels(xlabels)

# vertikale Linien
plt.vlines(xi, ymin=0, ymax=yi, color='C1', alpha=0.3)

sns.despine()
plt.legend();

Numerische Ableitung

In Differentialgleichungen werden Ableitungen verwenden, z.B.

\[ \sf y'(x) = \frac{dy(x)}{dx} \]

Zur numerischen Lösung wird die Differentialgleichung in eine algebraische Gleichung umgewandelt, indem Differenzenformeln für die Ableitungen verwendet werden. Aufgrund der Diskretisierung ist die Schrittweite \(\sf h\) durch die Gitterweite \(\sf \Delta x\) bereits vorgegeben. Somit wird nur auf die vorgehaltenen Funktionswerte zurückgegriffen.

Die Ableitungsfunktion ist somit z.B. mit der zentralen Differenzenformel zweiter Ordnung gegeben durch

\[ \sf y'(x_i) = \frac{y(x_{i+1}) - y(x_{i-1})}{2\Delta x} = \frac{y_{i+1} - y_{i-1}}{2\Delta x} \]

Bei der Berechnung der Randwerte, d.h. für \(\sf i=0\) und \(\sf i=n\) stehen nicht alle notwendigen Funktionswerte zur Verfügung. Hier muss auf die einseitigen Differenzenformeln zurückgegriffen werden. D.h.

\[\sf y'(x_0) = \frac{y_1 - y_0}{\Delta x} \]

\[\sf y'(x_n) = \frac{y_n - y_{n-1}}{\Delta x} \]

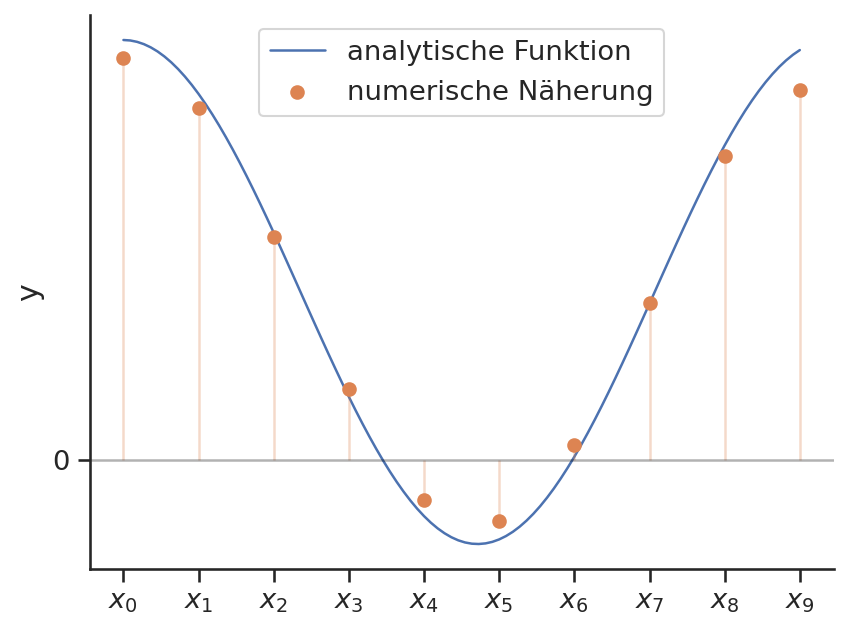
Für die obige Beispielfunktion und deren Diskretisierung ergibt sich folgende numersiche Ableitung.

# Anlegen eines Arrays, welches die gleiche Form hat wie die 
# Diskretisierung
ypi = np.zeros_like(xi)

# Berechnung der numerischen Ableitung
# Randwert i=0
ypi[0] = (yi[1] - yi[0]) / dx
# innerer Bereich i=1...n-2
ypi[1:-1] = (yi[2:] - yi[:-2]) / (2*dx)
# Randwert i=n
ypi[-1] = (yi[-1] - yi[-2]) / dx

# für die Visualisierung der analytischen Ableitungsfunktion
yp = 3*np.cos(3*x) + 2

# Darstellung der Daten
plt.plot(x, yp, label='analytische Funktion')
plt.scatter(xi, ypi, c='C1', label='numerische Näherung', zorder=3)

# einfache y-Achsen-Beschriftung
ax = plt.gca()
plt.yticks([0])
plt.ylabel('y')
ax.set_xticklabels(['0'])

# angepasste x-Achsen-Beschriftung
ax.set_xticks(xi)
xlabels = []
for i in range(n):
    xlabels.append(f'$x_{i}$')
ax.set_xticklabels(xlabels)

# vertikale Linien
plt.vlines(xi, ymin=0, ymax=ypi, color='C1', alpha=0.3)

# Nulllinie
plt.axhline(y=0, color='Black', alpha=0.3)

sns.despine()
plt.legend();

/tmp/ipykernel_6034/387181503.py:12: UserWarning: set_ticklabels() should only be used with a fixed number of ticks, i.e. after set_ticks() or using a FixedLocator.
  ax.set_xticklabels(['0'])