4.6. Temperaturgleichung#
Die Lösung einer gewöhnlichen Differentialgleichung, hier der Temperaturentwicklung, wird in dieser Aufgabe nochmals vorgestellt. Dabei wird die Gleichung erweitert und ein komplexer Quellterm implementiert.
Aufgabenteil A#
In der Vorlesung wurde folgende Differentialgleichung vorgestellt.
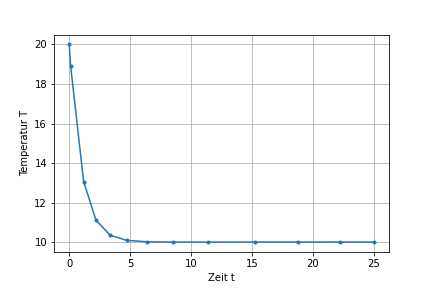
Verwenden Sie die Funktion scipy.integrate.solve_ivp um die Gleichung für \(\sf T_0 = 20\) mit \(\sf T_\infty=10\) und \(\sf Q=0\) zu lösen. Die Lösung soll bis \(\sf t=25\) berechnet werden. Erstellen und beschriften Sie den Lösungsplot.
Lösungshinweis#
Die Ausgabe könnte wie folgt aussehen.
Lösungsvorschlag#
Show code cell content
import numpy as np
import matplotlib.pyplot as plt
import scipy.integrate
Show code cell content
# Rechte-Hand-Seite der Gleichung, hier mit Q=0
def f_T1(t, T):
Tinfty = 10
return -(T-Tinfty)
Show code cell content
# Anfangswert der Lösung
T0 = 20
# Aufruf des Lösers
res1 = scipy.integrate.solve_ivp(f_T1, [0, 25], [T0])
Show code cell content
plt.plot(res1.t, res1.y[0], marker='.')
plt.xlabel("Zeit t")
plt.ylabel("Temperatur T")
plt.grid()
# Ausgabe für den Lösungshinweis
# plt.savefig('teil1.png')
Aufgabenteil B#
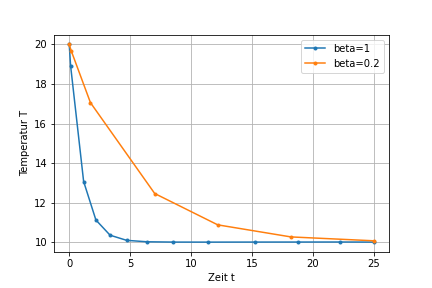
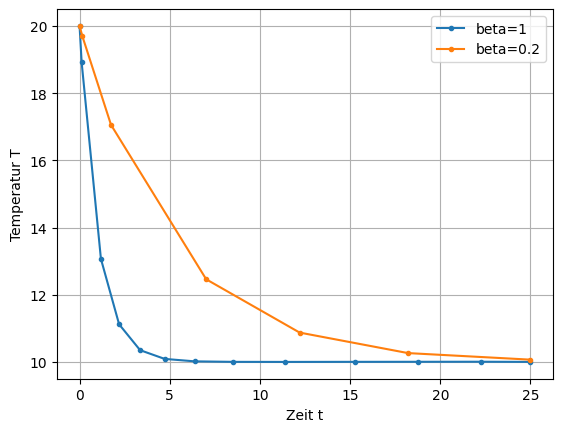
Fügen Sie einen neuen Koeffizienten \(\sf \beta\) als Vorfaktor vor den ersten Term auf der rechten Seite der Gleichung. Lösen Sie nun die Gleichung für \(\sf \beta=0.2\). Stellen Sie graphisch die Lösungen mit und ohne das \(\sf \beta\) in einer Graphik dar.
Lösungshinweis#
Die Ausgabe könnte wie folgt aussehen.
Lösungsvorschlag#
Show code cell content
def f_T2(t, T):
Tinfty = 10
beta = 0.2
return -beta*(T-Tinfty)
Show code cell content
T0 = 20
res2 = scipy.integrate.solve_ivp(f_T2, [0, 25], [T0])
Show code cell content
plt.plot(res1.t, res1.y[0], marker='.', label='beta=1')
plt.plot(res2.t, res2.y[0], marker='.', label='beta=0.2')
plt.xlabel("Zeit t")
plt.ylabel("Temperatur T")
plt.grid()
plt.legend()
# Ausgabe für den Lösungshinweis
# plt.savefig('teil2.png')
<matplotlib.legend.Legend at 0x7f813d34eb00>
Aufgabenteil C#
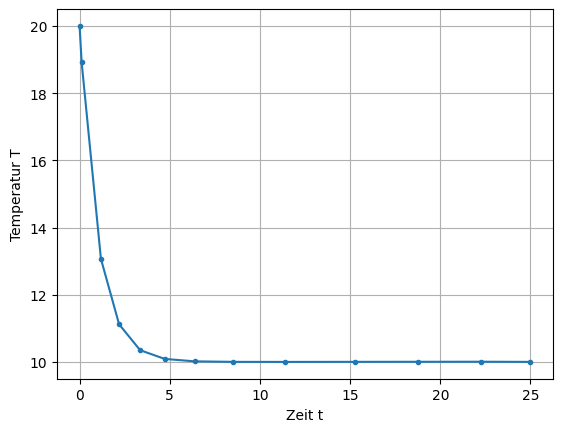
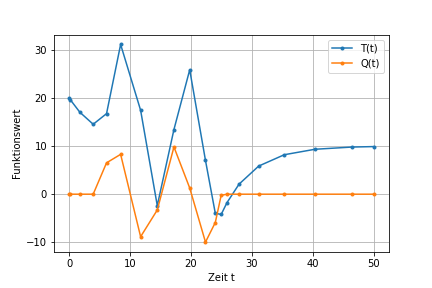
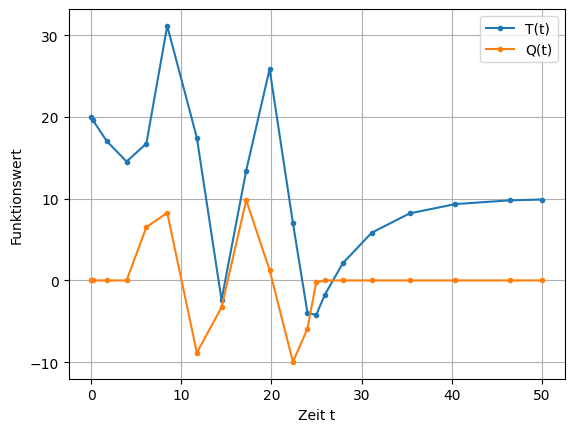
Nun wird der Quellterm \(\sf Q(t)\) erweitert. Dieser soll für die Zeit zwischen 5 und 25 zwei volle Sinus-Schwingungen mit einer Amplitude von 10 durchführen, sonst ist er Null. Lösen Sie die Gleichung mit \(\sf \beta=0.2\) bis zur Zeit \(\sf t=50\). Stellen Sie neben der Lösung auch die Quelltermfunktion \(\sf Q(t)\) in einer gemeinsamen Graphik dar.
Lösungshinweis#
Die Ausgabe könnte wie folgt aussehen.
Lösungsvorschlag#
Show code cell content
def f_Q(t):
Q = 0
if t >= 5 and t <= 25:
Q = 10 * np.sin((t-5)/20 * 4 * np.pi)
return Q
Show code cell content
def f_T3(t, T):
Tinfty = 10
return -0.2*(T-Tinfty) + f_Q(t)
Show code cell content
T0 = 20
res3 = scipy.integrate.solve_ivp(f_T3, [0, 50], [T0])
Show code cell content
plt.plot(res3.t, res3.y[0], marker='.', label='T(t)')
Q = np.zeros_like(res3.t)
for i in range(len(Q)):
Q[i] = f_Q(res3.t[i])
plt.plot(res3.t, Q, marker='.', label='Q(t)')
plt.xlabel("Zeit t")
plt.ylabel("Funktionswert")
plt.grid()
plt.legend()
# Ausgabe für den Lösungshinweis
# plt.savefig('teil3.png')
<matplotlib.legend.Legend at 0x7f813d3b7d60>
Aufgabenteil D#
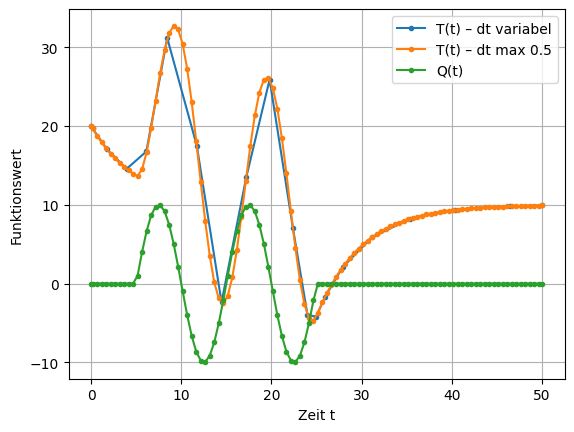
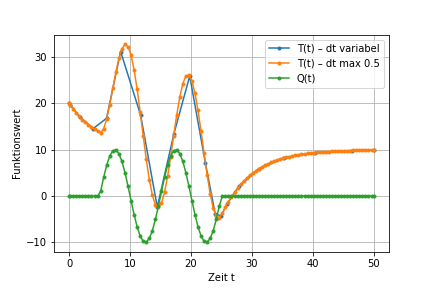
Die graphische Darstellung, siehe Lösungshinweis, deutet auf eine sehr sprunghafte Lösung. Verwenden Sie das optionale Argument max_step der Funktion scipy.integrate.solve_ivp um einen kleineren Zeitschritt, z.B. \(\sf \Delta t=0.25\), zu wählen. Vergleichen Sie nun die beiden Lösungen.
Lösungshinweis#
Die Ausgabe könnte wie folgt aussehen.
Lösungsvorschlag#
Show code cell content
T0 = 20
res4 = scipy.integrate.solve_ivp(f_T3, [0, 50], [T0], max_step=0.5)
Show code cell content
plt.plot(res3.t, res3.y[0], marker='.', label='T(t) – dt variabel')
plt.plot(res4.t, res4.y[0], marker='.', label='T(t) – dt max 0.5')
Q = np.zeros_like(res4.t)
for i in range(len(Q)):
Q[i] = f_Q(res4.t[i])
plt.plot(res4.t, Q, marker='.', label='Q(t)')
plt.xlabel("Zeit t")
plt.ylabel("Funktionswert")
plt.grid()
plt.legend()
# Ausgabe für den Lösungshinweis
# plt.savefig('teil4.png')
<matplotlib.legend.Legend at 0x7f813c1775e0>