2.1. Markdown#
Um auch mit reinen Textdateien eine formatierte Ausgabe zu ermöglichen, kann die Formatierung mit festgelegten Zeichen und deren Anordnung erfolgen. Eine populäre Möglichkeit, welche auch in Jupyter Anwendung findet, ist Markdown.
Grundlagen und Beispiele#
Markdown wird für die Erstellung von einfach formatierten Texten und oft auch im Internet verwendet. Die angebotenen Möglichkeiten decken bereits ein breites Spektrum ab und für die Erstellung wird einzig ein Texteditor benötigt.
In Jupyter-Notebooks können neben Code-Zellen auch Markdown-Zellen zur Dokumentation bzw. Beschreibung genutzt werden. Dazu muss der Zelltyp auf Markdown gesetzt werden, dies kann auch mit der Taste m erfolgen. Zum bearbeiten der Zelle kann diese per Doppelklick oder Enter aktiviert werden. Um den Markdown Text zu interpretieren, muss die Zelle, genauso wie beim Code, ausgeführt werden, also z.B. mit Shift-Enter oder Ctrl-Enter.
Beispielsweise kann Text in fett und kursiv dargestellt werden. Dies wird durch die Verwendung von * ermöglicht. Dieser Satz würde in Markdown wie folgt aussehen:
Beispielsweise kann Text in **fett** und *kursiv*
dargestellt werden.
Aufgabenteil A#
Schauen Sie sich die Dokumentation von Markdown an und erzeugen Sie folgende Ausgabe, wobei der blau gekennzeichnete Link zur Webseite der Bergischen Universität Wuppertal führen soll:

Lösungsvorschlag#
## Vorstellung
Mein Name ist **Max Mustermann** und ich arbeite an der [Bergischen
Universität Wuppertal](https://www.uni-wuppertal.de/).
## Aufgaben
Meine *eigentlichen* Aufgaben sind:
* Lehre
* Forschung
* Administration
## Programmierung
Ich programmiere gern mit Python und das sind meine liebsten
Programmzeilen:
```
mein_text = "Hallo Welt!"
print( mein_text )
```
Aufgabenteil B — Optional#
Mathematische Ausdrücke können in Markdown nicht dargestellt werden. Dazu unterstützen jedoch viele Markdown-Interpreter das Textsatzsystem LaTeX. Das Haupteinsatzgebiet von LaTeX liegt in der Erstellung von wissenschaftlichen Texten, z.B. Abschlussarbeiten oder Publikationen.
Um einen mathematischen Ausdruck hinzuzufügen, gibt es zwei Möglichkeiten:
als Teil einer Zeile, eingeschlossen durch
$oder als eigenständige Zeile, eingeschlossen durch
$$.
Beispiel einer eingebetteten Gleichung, wie \(a=b^2\), oder einer eigenständigen Zeile
Beispiel einer eingebetteten Gleichung, wie $a=b^2$, oder
einer eigenständigen Zeile
$$ a^2 + b^2 = c^2. $$
Sonderzeichen oder mathematische Objekte, werden mit einem \ eingeleitet und Gruppen von Anweisungen mit {} eingeschlossen. Die Kurzeinführung in mathematische Ausdrücke in LaTex kann hierzu einen Einstiegspunkt liefern.
Einige häufig eingesetzte Befehle:
Textposition,
^und_, z.B.a^{n+1}_kwird zu \(a^{n+1}_k\)griechische Buchstaben,
\alpha,\beta, etc.: \(\alpha, \beta\)Pfeile und Punkte, z.B.
\rightarrow,\cdot: \(a \rightarrow b \cdot c\)Summe, Integral,
\sum,\int: \(\int_0^{x_n} \phi\ d\phi \approx \sum_{i=0}^\infty x^i\)Brüche,
\frac{}{}: \(\frac{a}{b} = \frac{\alpha}{1 + \frac{1}{n}} \)
Benutzten Sie LaTeX um folgende Formel darzustellen:
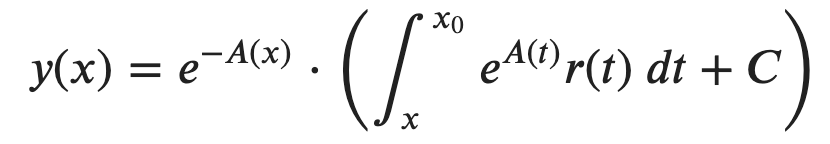
Lösungsvorschlag#
$$ y(x) = e^{-A(x)} \cdot \left(\int_x^{x_0} e^{A(t)}r(t)\ dt + C\right) $$`
