4.1.3. Monte-Carlo

Show code cell source Hide code cell source

import numpy as np
np.set_printoptions(precision=2, linewidth=65)

import matplotlib.pyplot as plt
plt.rc('figure', dpi=150)

import seaborn as sns
sns.set()
sns.set_style('ticks')
sns.set_context("notebook", font_scale=1.2, rc={"lines.linewidth": 1.2})

import scipy

Ein ganz anderer Ansatz zur Integration wird mit dem Monte-Carlo-Ansatz verfolgt. Hierbei werden Zufallspunkte \(\sf x_i\) innerhalb der gesuchten Integralbereichs generiert. Der Mittelwert der dazugehörigen Summe der Funktionswerte \(\sf f(x_i)\) nähert das Integral an. Insbesondere für eine kleine Anzahl von Zufallswerten kann das Ergebnis deutlich vom exakten Wert abweichen. Der Vorteil des Verfahrens wird bei hochdimensionalen Integralen deutlich.

Für \(\sf n \gg 1\) zufällige Stützstellen \(\sf x_i \in [a, b]\) gilt folgende Näherung

\[\sf I = \int_a^b f(x)\ dx \approx \frac{b-a}{n}\sum_{i=1}^n f(x_i) \]

Für das Beispiel aus den vorhergehenden Kapiteln gilt

def fkt(x):
    return np.sin(3*x) + 2*x

# Daten für die Visualisierung
x = np.linspace(0, 2, 100)
y = fkt(x)

# Exakte Lösung
I_exakt = (-1/3*np.cos(3*2) + 2**2) - (-1/3)

n = 2000
xi = np.random.random(n) * 2
yi = fkt(xi)
I = 2 * 1/n * np.sum(yi)
print(f"Integralwert für {n} Stützstellen: {I:.4f}")

Integralwert für 2000 Stützstellen: 4.0394

n_max = 50000
dn = 250
ns = np.arange(dn, n_max, dn, dtype=int)
mc = np.zeros(len(ns))

xi = np.zeros(n_max)

for i, n in enumerate(ns):
    xi[n-dn:n] = np.random.random(dn) * 2
    yi = fkt(xi[:n])
    mc[i] = 2 * 1/n * np.sum(yi)

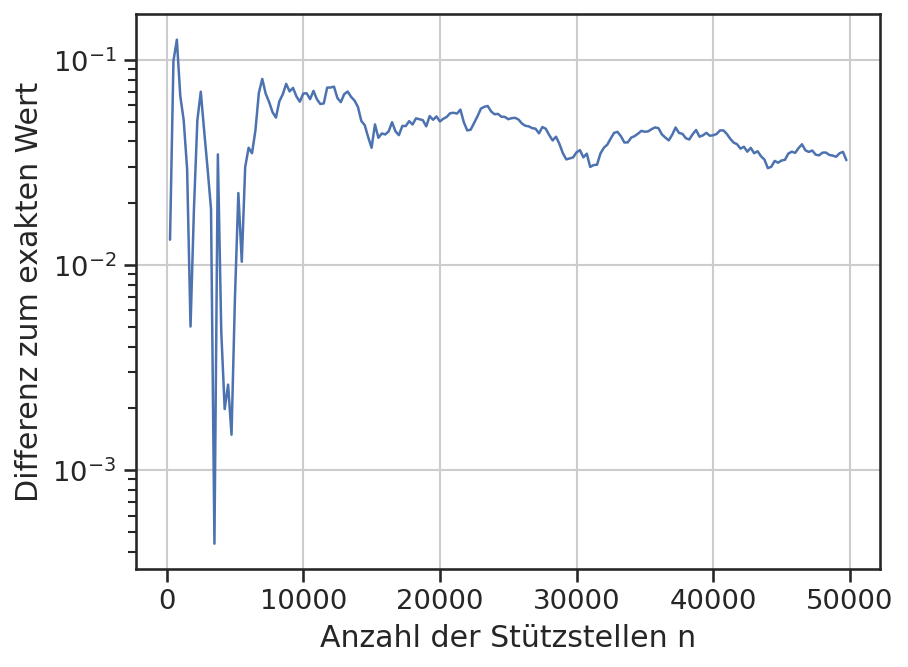
plt.plot(ns, np.abs(mc-I_exakt))

plt.xlabel('Anzahl der Stützstellen n')
plt.ylabel('Differenz zum exakten Wert')

# plt.xscale('log')
plt.yscale('log')

plt.grid();

Alternativ kann auch das Flächenverhältnis zwischen der zu integrierenden Funktion und einer Referenzfläche \(\sf A_r\) gebildet werden. Hierzu werden \(\sf n\) Zufallszahlenpaare \(\sf (x_i, y_i)\) generiert und gezählt wieviele davon in der gesuchten Fläche liegen. Die Annahme ist, dass sich beide Verhältnisse für große \(\sf n\) annähern. Im einfachsten Fall, wenn \(\sf f(x) \ge 0\), gilt folgende Abschätzung

\[\sf I \approx \frac{A_r \cdot \left|\left\{y_i \ |\ y_i < f(x_i)\right\}\right|}{n} \]

Im obigen Beispiel kann die Fläche \(\sf[0, 2] \times [0, 4] = 8\) als Referenzfläche verwendet werden.

n = 2000
xi = np.random.random(n) * 2
yi = np.random.random(n) * 4

z = np.sum(yi < fkt(xi))

I = z / n * 8
print(f"Integralwert für {n} Stützstellen: {I}")

Integralwert für 2000 Stützstellen: 4.156

n_max = 50000
dn = 250
ns = np.arange(dn, n_max, dn, dtype=int)
mc = np.zeros(len(ns))

xi = np.zeros(n_max)
yi = np.zeros(n_max)

for i, n in enumerate(ns):
    xi[n-dn:n] = np.random.random(dn) * 2
    yi[n-dn:n] = np.random.random(dn) * 4
    z = np.sum(yi[:n] < fkt(xi[:n]))
    mc[i] = z / n * 8

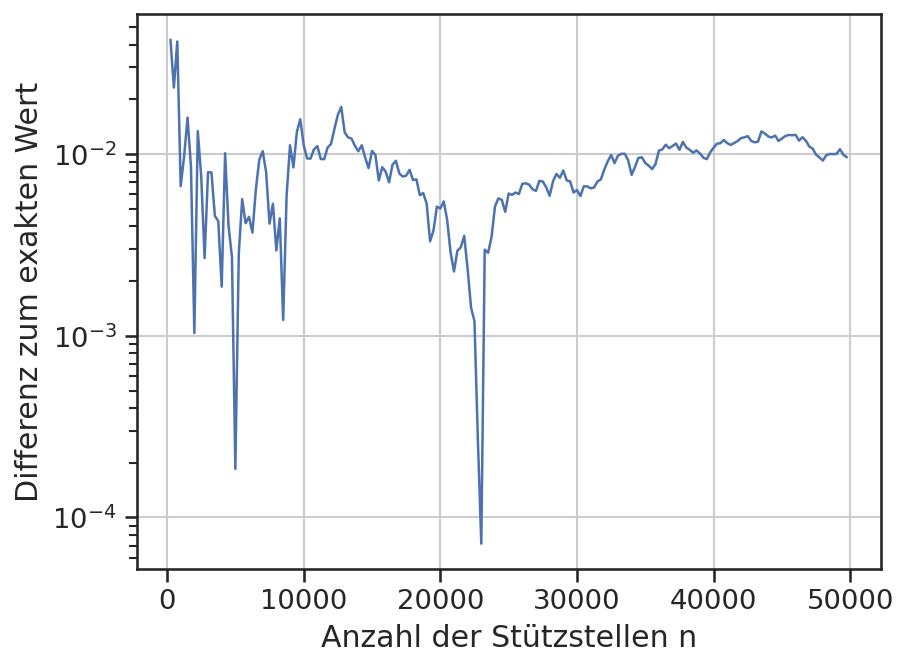
plt.plot(ns, np.abs(mc-I_exakt))

plt.xlabel('Anzahl der Stützstellen n')
plt.ylabel('Differenz zum exakten Wert')

# plt.xscale('log')
plt.yscale('log')

plt.grid();