4.3.3. Partielle DGL

Show code cell source Hide code cell source

import numpy as np
np.set_printoptions(precision=2, linewidth=65)

import matplotlib.pyplot as plt
plt.rc('figure', dpi=150)

import seaborn as sns
sns.set()
sns.set_style('ticks')
sns.set_context("notebook", font_scale=1.2, rc={"lines.linewidth": 1.2})

import scipy.integrate

Als Beispiel für die Lösung einer partiellen Differentialgleichung wird die eindimensionale Wärmeleitgleichung für \(\sf T = T(x,t)\) genutzt.

\[ \sf \partial_t T(x,t) = \partial_{xx}T(x,t) \]

In dieser Darstellung wurde die häufig Verwendete verkürzte Schreibweise für partielle Ableitungen verwendet

\[ \sf \partial_t = \frac{\partial}{\partial t} \quad \partial_{xx} = \frac{\partial^2}{\partial x^2} \]

Zur numerischen Lösung werden die beiden Ableitungen mit finiten Differenzen angenährt. Die zeitliche Ableitung wird mit der Vorwärtsdifferenzenformel zu

\[\sf \frac{T(x)^{n+1} - T(x)^n}{\Delta t} = \partial_{xx}T(x,t) \]

Die Ortsableitung wird mit der Differenzenformel für die zweite Ableitung angenährt. Dabei wird insgesamt wieder das explizite Euler-Verfahren verwendet, so dass die rechte Seite der Gleichung zum Zeitpunkt \(\sf n\) ausgewertet wird. Damit ergibt sich für einen Stützpunkt \(\sf i\) zur Zeit \(\sf n\)

\[\sf \frac{T^{n+1}_i - T^n_i}{\Delta t} = \frac{T^n_{i-1} - 2T^n_i + T^n_{i+1}}{\Delta x^2} \]

Und die Auflösung nach \(\sf T^{n+1}_i\) führt zu

\[\sf T^{n+1}_i = T^n_i + \Delta t\frac{T^n_{i-1} - 2T^n_i + T^n_{i+1}}{\Delta x^2} \]

Damit sind alle Bestandteile eines einfachen expliziten Lösers für die obige Wärmeleitgleichung gegeben. Die Lösung soll auf dem Intervall \(\sf [0, x_{ende}]\times[0, t_{ende}]\) erfolgen.

Als Beispiel wird der Anfangswert für die Temperatur \(\sf T(x, t=0) = 0\) angenommen und die Randbedinungen sind \(\sf T(x=0, t) = 1\) und \(\sf T(x=x_{ende},t) = 0\). Die örtliche Ausdehnung ist \(\sf x_{ende}=100\) und die Berechnung soll bis zum Zeitpunkt \(\sf t_{ende}=5000\) erfolgen, wobei 100 Stützstellen für \(\sf x\) und 10000 für \(\sf t\) verwendet werden sollen.

# Konstanten für das Beispiel
x_ende = 100
t_ende = 5000
nx = 100
nt = 10000
dx = x_ende / (nx-1)
dt = t_ende / (nt-1)

# Infos für die Visualisierung
x = np.linspace(0, x_ende, nx)
t = np.linspace(0, t_ende, nt)

# Array auf dem die Gesamtlösung gespeichert wird
T = np.zeros((nt, nx))

# Setzen der Anfangswerte
T[0,:] = 0

for n in range(1, nt-1):
    Tc = T[n]
    Tn = T[n+1]

    Tn[1:-1] = Tc[1:-1] + dt*(Tc[:-2] - 2*Tc[1:-1] + Tc[2:])/dx**2

    Tn[0] = 1
    Tn[-1] = 0

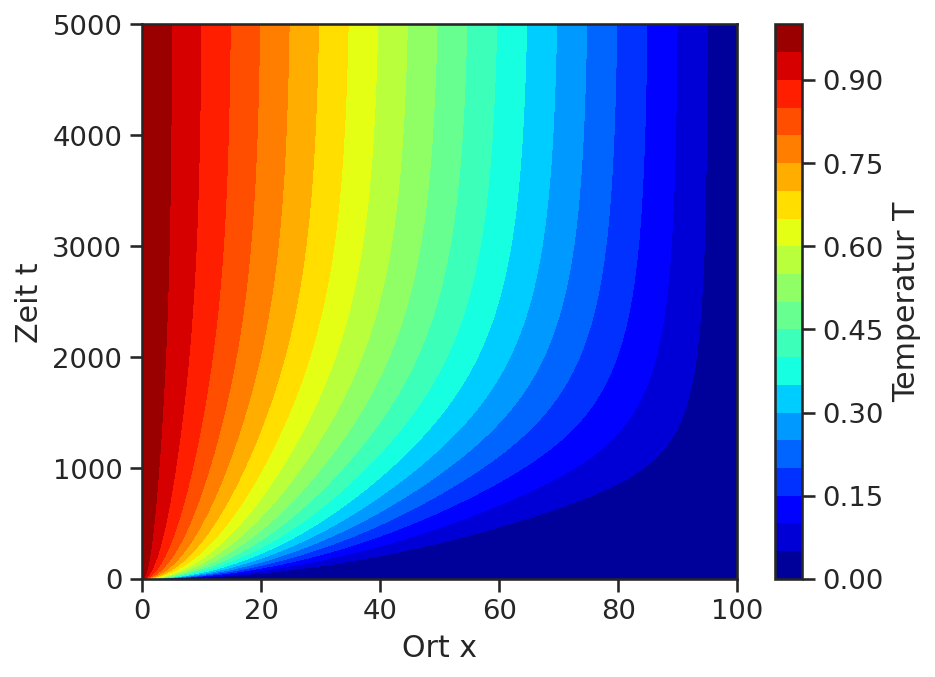
plt.contourf(T, levels=20, extent=[0, x_ende, 0, t_ende], cmap='jet')
plt.xlabel('Ort x')
plt.ylabel('Zeit t')
plt.colorbar(label='Temperatur T')

<matplotlib.colorbar.Colorbar at 0x7f1aab16e830>

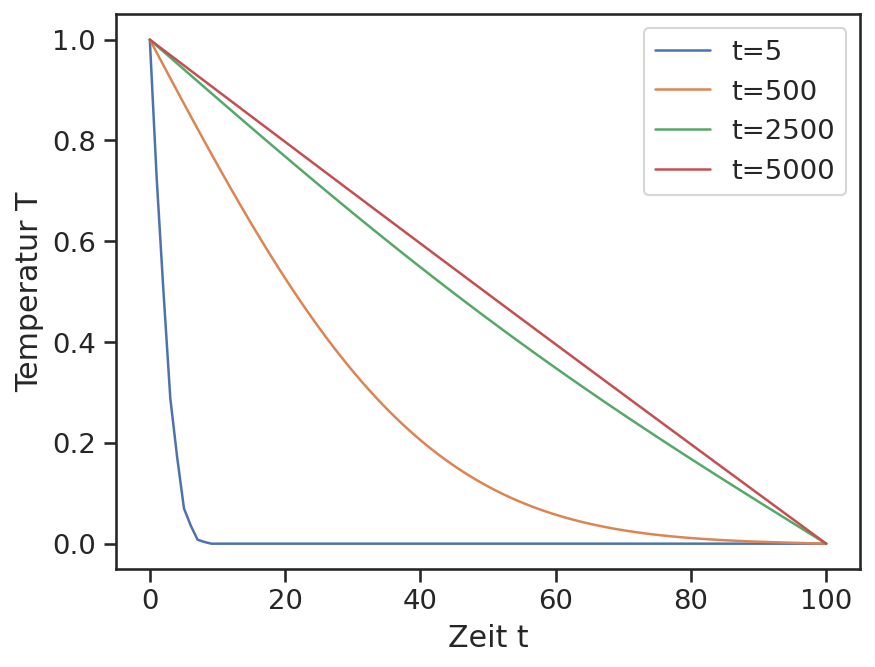
for i in [nt//1000, nt//10, nt//2, -1]:
    t_label = f't={t[i]:.0f}'
    plt.plot(x, T[i], label=t_label)

plt.legend()
plt.xlabel('Zeit t')
plt.ylabel('Temperatur T');

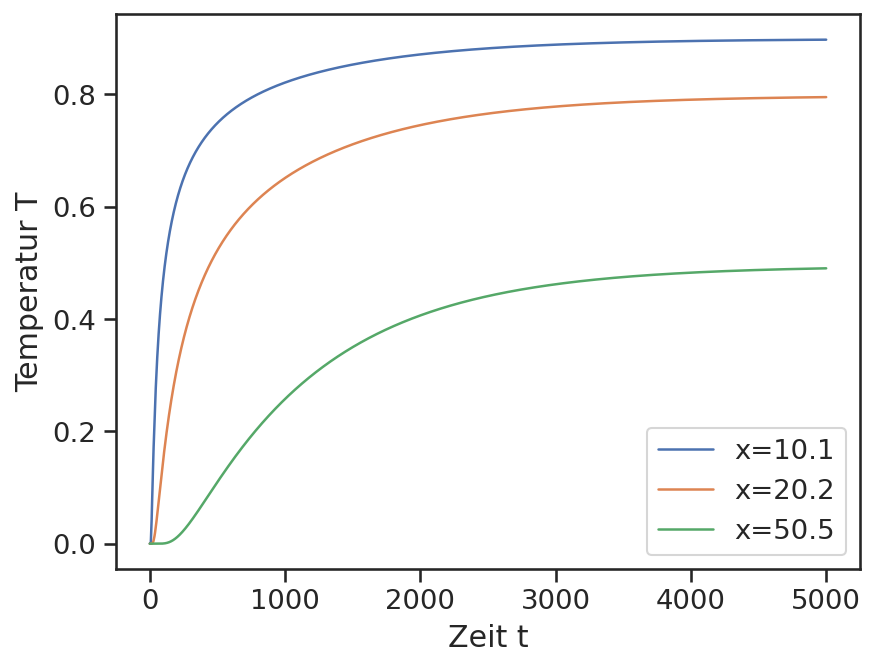
for i in [nx//10, nx//5, nx//2]:
    x_label = f'x={x[i]:.1f}'
    plt.plot(t, T[:,i], label=x_label)

plt.legend()
plt.xlabel('Zeit t')
plt.ylabel('Temperatur T');