3.2.6. Bilddaten#
Digitale Bilder bestehen aus drei Farbwerten (rot, grün, blau) pro Pixel, d.h. Bildelement. Aus diesen drei Werten wird bei der Darstellung die gewünschte Farbe zusammengestellt. Der Wertebereich ist dabei entweder zwischen 0 und 255 (8-bit) oder als Gleitkommazahl zwischen 0 und 1.
import numpy as np
np.set_printoptions(precision=2, linewidth=65)
import matplotlib.pyplot as plt
plt.rc('figure', dpi=150)
Im weiteren wird ein Bild vom Campus Haspel campus_haspel.jpeg zur Demonstration verwendet. Die Bilddaten können mit der plt.imread-Funktion als dreidimensionales Array von 8-bit vorzeichenlosen ganzen Zahlen eingelesen werden.
data = plt.imread('./campus_haspel.jpeg')
print( "Form:", data.shape )
print( "Datentyp der Elemente:", data.dtype)
Form: (3024, 4032, 3)
Datentyp der Elemente: uint8
# Auszug aus den dreidimensionalem Datensatz
print( data )
[[[ 52 42 43]
[ 46 36 37]
[ 42 33 34]
...
[ 58 46 32]
[ 54 37 21]
[ 50 32 12]]
[[ 46 37 38]
[ 43 35 33]
[ 41 35 35]
...
[ 58 46 34]
[ 59 43 27]
[ 51 34 16]]
[[ 37 33 30]
[ 38 35 30]
[ 40 36 33]
...
[ 50 40 28]
[ 53 39 26]
[ 55 42 26]]
...
[[125 106 91]
[122 105 89]
[121 105 89]
...
[ 9 14 10]
[ 5 14 9]
[ 9 20 14]]
[[129 96 87]
[123 95 84]
[112 94 80]
...
[ 12 14 11]
[ 4 14 6]
[ 5 16 8]]
[[134 95 88]
[132 99 90]
[120 101 87]
...
[ 12 14 11]
[ 7 14 7]
[ 4 15 7]]]
Mit der bereits vorgestellten Funktion plt.imshow kann das Bild in Echtfarben dargestellt werden. Dies funktioniert, da die Funktion die einzelnen Ebenen, hier der letzte Index, des Datensatzes als Farbinformationen (rot, grün, blau) interpretiert. Wäre noch eine vierte Ebene dabei, würde sie als individueller Transparenzwert verwendet worden.
plt.imshow( data );

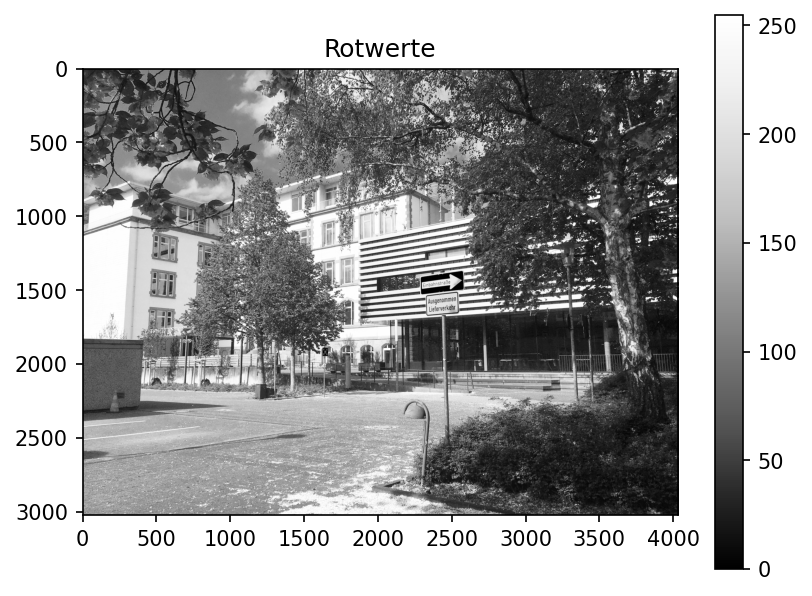
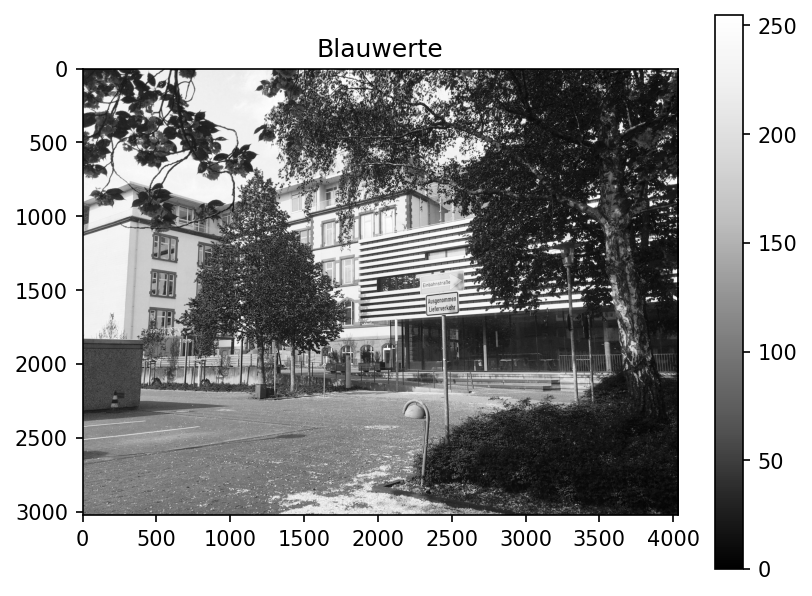
Natürlich können auch die einzelnen Farbebenen individuell betrachtet werden. Dazu wird der letzte Index festgehalten.
titel = ["Rotwerte", "Grünwerte", "Blauwerte"]
for i in range(3):
# Als Farbskale wird die invertierte '_r' Grauskala
# verwendet 'Greys'
plt.imshow( data[:,:,i], cmap='Greys_r' )
plt.title(titel[i])
plt.colorbar()
plt.show()

Da die Bilddaten als Arrays gespeichert sind, sind viele der möglichen Optionen, z.B. zur Teilauswahl oder Operationen, verfügbar. Das untere Beispiel zeigt einen Ausschnitt im Rotkanal des Bildes.
bereich = np.array(data[1320:1620, 400:700, 0], dtype=float)
plt.imshow( bereich, cmap="Greys_r" )
plt.colorbar();

Als Beispiel für eine Bildoperation wird der Laplace-Operator vorgestellt. Er kann genutzt werden um Ränder von Objekten zu identifizieren. Dazu wird für jeden Bildpunkt \(\sf B_{i,j}\) – außer an den Rändern – folgender Wert \(\sf \phi_{i, j}\) berechnet:
Folgende Funktion implementiert diese Operation. Darüber hinaus werden alle Werte von \(\sf \phi\) unterhalb eines Schwellwerts auf Null und oberhalb auf 255 gesetzt.
def img_lap(data, schwellwert=25):
# Erstellung einer Kopie der Daten, nun jedoch als
# Array mit Gleitkommazahlen
bereich = np.array(data, dtype=float)
# Aufteilung der obigen Gleichung in zwei Teile
lapx = bereich[2:, :] - 2*bereich[1:-1, :] + bereich[:-2, :]
lapy = bereich[:, 2:] - 2*bereich[:, 1:-1] + bereich[:, :-2]
# Zusammenführung der Teile und Bildung des Betrags
lap = np.abs(lapx[:,1:-1] + lapy[1:-1, :])
# Schwellwertanalyse
lap[lap > schwellwert] = 255
lap[lap < schwellwert] = 0
return lap
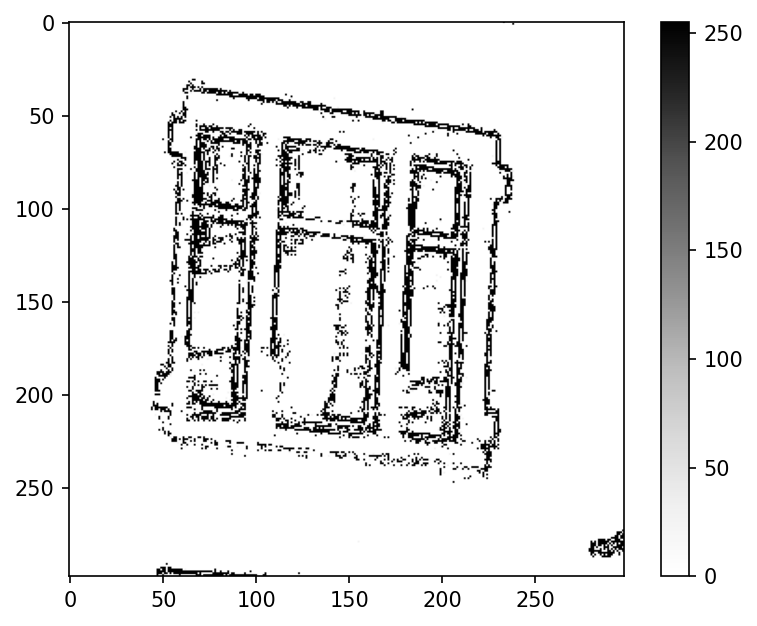
Die Anwendung des Laplace-Operators auf den oberen Bildausschnitt ergibt folgende Ausgabe. Hier sind deutlich die Umrisse der Bildstrukturen erkennbar.
lap = img_lap(bereich)
plt.imshow(lap, cmap="Greys")
plt.colorbar();
Zum Vergleich noch beide Abbildungen nebeneinander. Im folgenden wird die Funktion plt.subplot verwendet, welche mehrere Graphiken in einer Abbildung ermöglicht. Beispiele und Dokumentation sind beispielsweise hier zu finden.
ax = plt.subplot(1, 2, 1)
ax.imshow(bereich, cmap="Greys_r")
ax = plt.subplot(1, 2, 2)
ax.imshow(lap, cmap="Greys");

